RでVARモデルを推定してインパルス応答関数を出す時に、インパルス応答関数が対応しているところの「ショック」の大きさが幾らなのかを、どこから得たらいいのかという疑問がわきました。

こういう図を見せられたとして、まぁ増えるのか減るのかさえ分かればいい場合が多いかもしれませんが、タテ軸の数字はレスポンス側の変数の値だから意味が分かるものの、これがインパルス側の変数の当期の値に「どれだけのショック」を与えた場合に生まれる変動なのか数字で言ってくれ、って頼まれたらどう答えるのかなと。
で、{vars}パッケージの仕様書を見ると、コレスキー分解をしているようなので、たぶんショック側の変数の「撹乱項の標準偏差」だろうと思うのですが、確かめ方が私には俄かには分からなかったので、不躾ながらパッケージの開発者(Bernhard Pfaff氏)にメールで「ショックの大きさは、撹乱項の標準偏差の推定値ってことで合ってますか?」と聞いてみました。
そしたら親切にも速攻で返事が返ってきて、「そのとおりや! "vars:::Psi.varest" と打って俺のPsiのコードを見とけ!」と言われました。
ここでいうPsiは、
https://cran.r-project.org/web/packages/vars/vars.pdf
この仕様書の28ページの上の方に載ってる式のΨのことで、この行列の中身が直交化インパルス応答に対応しています。なおこれはVARのVMA表現ですね。*1
で、コードをみてみると、
> vars:::Psi.varest function (x, nstep = 10, ...) { if (!(class(x) == "varest")) { stop("\nPlease provide an object of class 'varest', generated by 'VAR()'.\n") } nstep <- abs(as.integer(nstep)) Phi <- Phi(x, nstep = nstep) Psi <- array(0, dim = dim(Phi)) params <- ncol(x$datamat[, -c(1:x$K)]) sigma.u <- crossprod(resid(x))/(x$obs - params) P <- t(chol(sigma.u)) dim3 <- dim(Phi)[3] for (i in 1:dim3) { Psi[, , i] <- Phi[, , i] %*% P } return(Psi) }
ここでsigma.uとなっているものが、残差の分散共分散行列ですね!
ということは、この行列と同じものを自分で求めて、対角要素の平方根を取ればショックの値になるはずです。
これは、VARモデルの推定結果であるx(varestクラスオブジェクト)の中に入っている残差の行列
resid(x)
を取り出してクロス積をとって自由度で割ったものです。
自由度は、元のデータがN変量×T期分あって、VAR(p)モデルを構築したのであれば、
df = (T-p) - (Np + 1) # +1は定数項の分
になります。
以下、念のため実際にサンプルデータで推定してみてやり方を確認しておくことにします。
まずデータを読み込みます。変数が4個ありますが、労働生産性と実質賃金だけ使おうと思います。
> library(vars) > > # 練習データのCanadaを時系列データ型でインポート > # e: 千人あたりの雇用 > # pros: 労働生産性 > # rw: 実質賃金 > # U: 失業率 > > data(Canada) > > # 私はts型に慣れてないのでデータフレームにしますw > canada <- as.data.frame(as.matrix(Canada)) >
どんなデータか描画しておきます。
> split.screen(c(2,1)) # 描画デバイス分割 > screen(1) > plot(canada$prod, type='l', main='Productivity') # 労働生産性 > screen(2) > plot(canada$rw, type='l', main='Real Wage') # 実質賃金
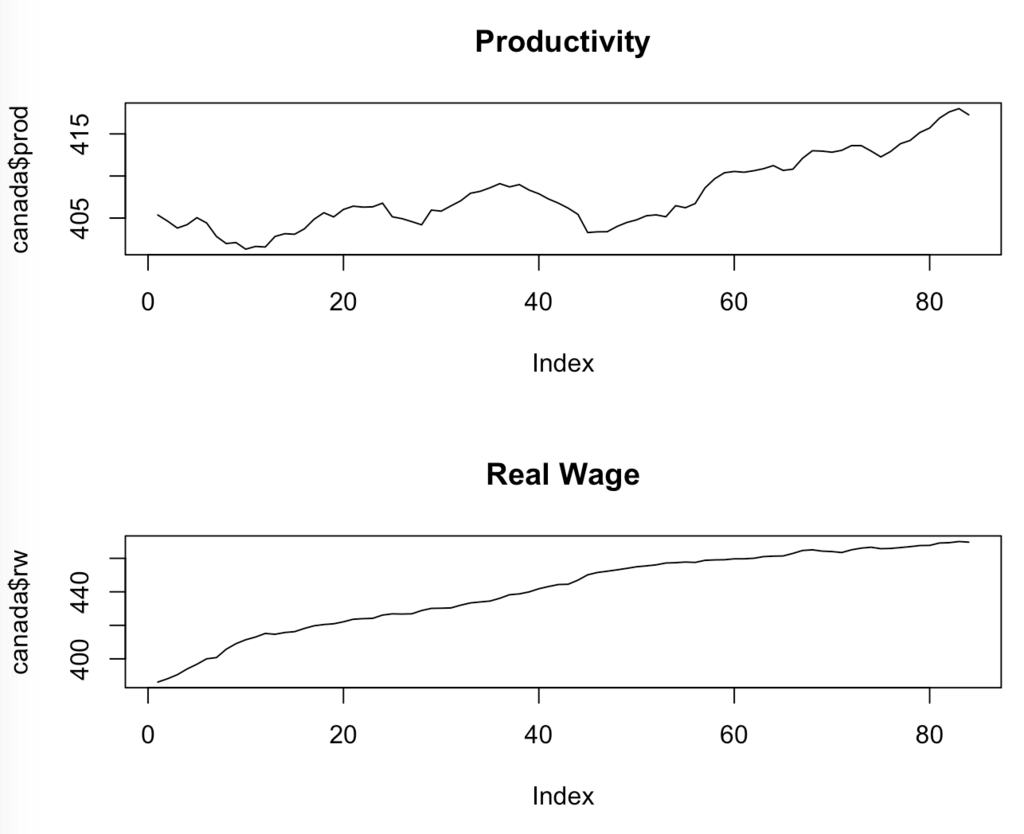
では、VARモデルを推定していきます。
簡単にするため、労働生産性(prod)と実質賃金(rw)という2つの変数だけでやってみます。
> ### 労働生産性と実質賃金のデータだけでVARモデルを構築します > # ラグの選択 > lag <- VARselect(canada[,c(2:3)], lag.max=10)$selection[1] # AIC最適ラグ数を選択 > print(lag) AIC(n) 3 > > # VARの推定 > var.canada <- VAR(canada[,c(2:3)], p=lag, type='const') > summary(var.canada) VAR Estimation Results: ========================= Endogenous variables: prod, rw Deterministic variables: const Sample size: 81 Log Likelihood: -174.944 Roots of the characteristic polynomial: 0.9843 0.813 0.813 0.5431 0.5431 0.4038 Call: VAR(y = canada[, c(2:3)], p = lag, type = "const") Estimation results for equation prod: ===================================== prod = prod.l1 + rw.l1 + prod.l2 + rw.l2 + prod.l3 + rw.l3 + const Estimate Std. Error t value Pr(>|t|) prod.l1 1.21318 0.11423 10.620 <2e-16 *** rw.l1 -0.02120 0.09222 -0.230 0.8188 prod.l2 -0.21853 0.18092 -1.208 0.2309 rw.l2 -0.14257 0.13835 -1.031 0.3061 prod.l3 -0.04157 0.11778 -0.353 0.7251 rw.l3 0.16883 0.08846 1.909 0.0602 . const 17.21994 10.69523 1.610 0.1116 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.6841 on 74 degrees of freedom Multiple R-Squared: 0.976, Adjusted R-squared: 0.974 F-statistic: 501.3 on 6 and 74 DF, p-value: < 2.2e-16 Estimation results for equation rw: =================================== rw = prod.l1 + rw.l1 + prod.l2 + rw.l2 + prod.l3 + rw.l3 + const Estimate Std. Error t value Pr(>|t|) prod.l1 -0.12808 0.13563 -0.944 0.34808 rw.l1 1.08616 0.10949 9.921 3.1e-15 *** prod.l2 -0.27601 0.21480 -1.285 0.20281 rw.l2 -0.17954 0.16426 -1.093 0.27793 prod.l3 0.44228 0.13984 3.163 0.00227 ** rw.l3 0.06736 0.10502 0.641 0.52323 const -3.05700 12.69828 -0.241 0.81042 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.8122 on 74 degrees of freedom Multiple R-Squared: 0.9987, Adjusted R-squared: 0.9985 F-statistic: 9176 on 6 and 74 DF, p-value: < 2.2e-16 Covariance matrix of residuals: prod rw prod 0.467974 0.002593 rw 0.002593 0.659676 Correlation matrix of residuals: prod rw prod 1.000000 0.004666 rw 0.004666 1.000000 >
VAR(3)の推定が終わりました。
次に「労働生産性→実質賃金」という方向の、直交インパルス応答関数を求めます。あわせてグラフの描画もしておきます。
> irf.canada <- irf(var.canada,impulse='prod', + response='rw', + ortho = TRUE, + n.ahead=10,ci=0.95, + cumulative = FALSE, + runs=300 + ) > > print(irf.canada$irf) $prod rw [1,] 0.003789932 [2,] -0.083499262 [3,] -0.386475239 [4,] -0.440968850 [5,] -0.394311432 [6,] -0.341204111 [7,] -0.296874634 [8,] -0.234418701 [9,] -0.160965629 [10,] -0.089254559 [11,] -0.023464820 > plot(irf.canada)

これでつまり、当期(第1期)のprod(労働生産性)に撹乱項の1標準偏差分のショックが加えられた時の、各期のrw(実質賃金)の増減が得られました。
で、問題は「その労働生産性の撹乱項1標準偏差分ってどんだけやねん」ということですが、これは次のようにして計算できます。回りくどい書き方ですが、
> # 自由度 > Obs <- var.canada$obs # 推定されるyの期数(元データの行数-ラグ次数) > N <- var.canada$K # 変数の数 > p <- lag # ラグ次数 > df <- Obs - (N*p + 1) > > # 残差の分散共分散行列 > sigma.u <- crossprod(resid(var.canada))/df > print(sigma.u) prod rw prod 0.467973610 0.002592639 rw 0.002592639 0.659676363 > > # irf()関数でそれぞれをimpulsに設定したときのショック=撹乱項の標準偏差 > shock.prod <- sqrt(sigma.u[1,1]) > shock.rw <- sqrt(sigma.u[2,2]) > > print(shock.prod) # prodの撹乱項1標準偏差分の値 [1] 0.684086 >
ここまでで、ショックの値は計算できました。
つまりさっきのインパルス応答関数と合わせていうと、当期の労働生産性の撹乱項に0.684086のショックを加えると、当期の実質賃金には0.003789932、2期目には-0.083499262...の影響があるということが分かったわけです。(実際は先に単位根とか共和分とかを見ないといけませんがここでは分析自体が目的ではないので省略。)
ちなみにこの撹乱項の標準偏差の値、どっかに入ってるのではないかと思って探してみたら、いちいち計算しなくても、以下のようにすれば一発で取り出すことができました。実務上はこれを使えばいいと思います*2。summaryをprintしたときの出力にも、'residual standard error'として載っています*3。
念のためですが、さっきのsigma.uの対角要素は分散、こっちのsigmaは標準偏差の推定値です。
> summary(var.canada)$varresult$prod$sigma [1] 0.684086 > > summary(var.canada)$varresult$rw$sigma [1] 0.8122046
念のため、これがインパルス応答関数のショックの値に使われているという理解であってるのかどうか、
沖本(2010).経済・ファイナンスデータの計量時系列分析,朝倉書店.
に書いてある方法に照らしながら手計算でインパルス応答を出してみて、それが{vars}パッケージのirf()関数の結果と確認するかを見ておきます。ただし後述の通り、使われているショックの値が合ってるかどうかを確認するだけなら、1年後、2年後…の逐次計算をしなくても、当期のresponseだけ見れば分かります。
まず、沖本(2010)のp.87-90あたりに書いてある「三角分解」(ほかの呼び方もあるようですが)の行列Aは、以下のように作れますね。
a <- sigma.u[2,1]/sigma.u[1,1] A <- matrix(c(1,a,0,1),2,2)
で、1つ目の変数から2つ目の変数*4へのインパルス応答のうち、「当期の値」(今回の例でいうと1期目のrwのレスポンスの値)については、「2つ目の変数の撹乱項のうち、1つ目の変数から影響を受けてる部分」がその値に一致すると思います。
沖本(2010)のp.89の、

この部分に「0.3u_1t」ってのがありますが、要するに2つ目の変数の撹乱項ってのは、2つ目の変数に固有の撹乱項と、1つ目の変数の撹乱項を0.3倍した成分に分かれるということですね。これを分けたのが直行化ってやつです。
で、インパルス応答関数とVARモデルの定義から言って、2つ目の変数の1期目のレスポンスには、1つ目の変数の1期目に与えられたショックを0.3倍(今回の場合でいうとa倍)した値だけが入ることになるので、これだけなら手計算がすぐできます。2期目以降の手計算は面倒ですが。
今回の例でいうと、以下のようになります。
> response.rw.1 <- a * shock.prod > print(response.rw.1) [1] 0.003789932 >
この通り、さっきの「0.003789932」と一致してるので、合ってると思います。
いつも忘れてしまうのですが、非直交化インパルス応答関数であれば、インパルス側の当期の値にショックがあっても、レスポンス側の当期の値は変わりません。しかし直交化インパルス応答関数は、インパルスとレスポンスの攪乱項同士に相関があることを仮定するものなので、当期のインパルス側変数にショックが入ると、当期のレスポンス側変数にもちょっとだけ影響があります。
Rで出力されるグラフの、「1」というのは当期のことで、「10」は第10期、つまり9期先ということですね。