Rで二段階最小二乗法の演習（『gretlで計量経済分析』を参考に）

『gretlで計量経済分析』という教科書があって、入門的な統計分析を非常にわかりやすく解説していると思いました。
学部レベルの人に統計分析を教える上では、関心の対象が政治や経済なのであれば、こういう「経済ネタ」で統計学が学べる本が良いのかもしれない。（私は最初は心理学系の本で勉強した。）
gretl（グレーテル）というソフトの使い勝手は私はよく知りませんが、見た感じ、初学者向けにはGUIもわかりやすくて良いんじゃないでしょうか。

ところで、第8章でごく簡単なマクロ経済モデルを材料にして二段階最小二乗法を実行するという演習があり、内生性の問題とその解決法としての操作変数法・二段階最小二乗法について説明するのに、なかなか分かりやすい事例だなと思いました。
しかし、gretlを使っていく予定はないので、以下のようにRで実行しました。

OLSでの推定

以下のように超単純なマクロモデルを考える。

Ct = α + βYt + ut
Yt = Ct + It

1つめの式を変形すると、
Yt = α/(1-β) + It/(1-β) + ut/(1-β)

ここで、
C:消費、Y:所得、I:投資、u:撹乱項、0 < β < 1

これらはようするに、消費は所得だけの関数として決まり、所得は、消費と投資の合計に一致する、というモデルを想定している。
最初の式で、説明変数にYtが入っているが、Ytにはutが入っているわけなので、説明変数と撹乱項が相関しており内生性があるということになる。内生性があると、OLSが一致推定になるための条件を満たさないので、サンプルサイズを増やしても真の値に近づいていかないことになる。そのためOLSでは妥当な推定ができない。

まずパラメータの真の値を自分で設定した上で、乱数で変数を作成し、生成された変数からOLSでパラメータを推定してみて、真の値とズレてしまう様子を確認する。

# ========== OLSで推定する ========== #

# まず、αとβの真の値を設定しておく。
alpha <- 2.5
beta <- 0.6

# 以下は、乱数からデータ系列をつくって、OLSで推定したパラメータを返すという処理を繰り返す関数。

repeat_ols <- function(para, n, T, sd){

  # あとで結果を並べるために設けておく空のベクトル
  alpha_output_ols <- c()
  beta_output_ols <- c()
  
  # 処理はn回繰り返させる
  for (i in 1:n) {
  
    # 投資Itは1から始まって毎期0.5ずつ増えることにする。全部でT期分。
    It <- seq(from=1, by=0.5, length.out=T)
    
    # 変形後の上式からYtをつくる。撹乱項utは正規乱数。
    set.seed(i)
    ut <- rnorm(n=T, mean=0, sd=sd)
    Yt <- (alpha/(1-beta)) + (It/(1-beta)) + (ut/(1-beta))

    # Ctをつくる
    Ct <- alpha + beta*Yt + ut
    
    # CをYに回帰してαとβをOLSで推定する。
    model_cy_ols <- lm(Ct ~ Yt)  # OLS推定
    alpha_est_ols <- model_cy_ols$coefficients[1]  # αの推定値
    beta_est_ols <- model_cy_ols$coefficients[2]  # βの推定値
    
    # 繰り返し推定した結果を並べておく
    alpha_output_ols <- c(alpha_output_ols, alpha_est_ols)
    beta_output_ols <- c(beta_output_ols, beta_est_ols)
    }
  
  # 出力
  if(para=='alpha'){
    return(alpha_output_ols)
  }
  if(para=='beta'){
  return(beta_output_ols)
  }
}

# 1000回推定して結果を取り出す
alpha_results_ols <- repeat_ols(para='alpha', n=1000, T= 100, sd=5)
beta_results_ols <- repeat_ols(para='beta', n=1000, T= 100, sd=5)

# 推定した1000個のα・βの平均を確認する
mean(alpha_results_ols)
mean(beta_results_ols)

> mean(alpha_results_ols)
[1] -0.4664703
> mean(beta_results_ols)
[1] 0.6419773

# ヒストグラムをかいてみる
hist(alpha_results_ols, breaks=20)
hist(beta_results_ols, breaks=20)

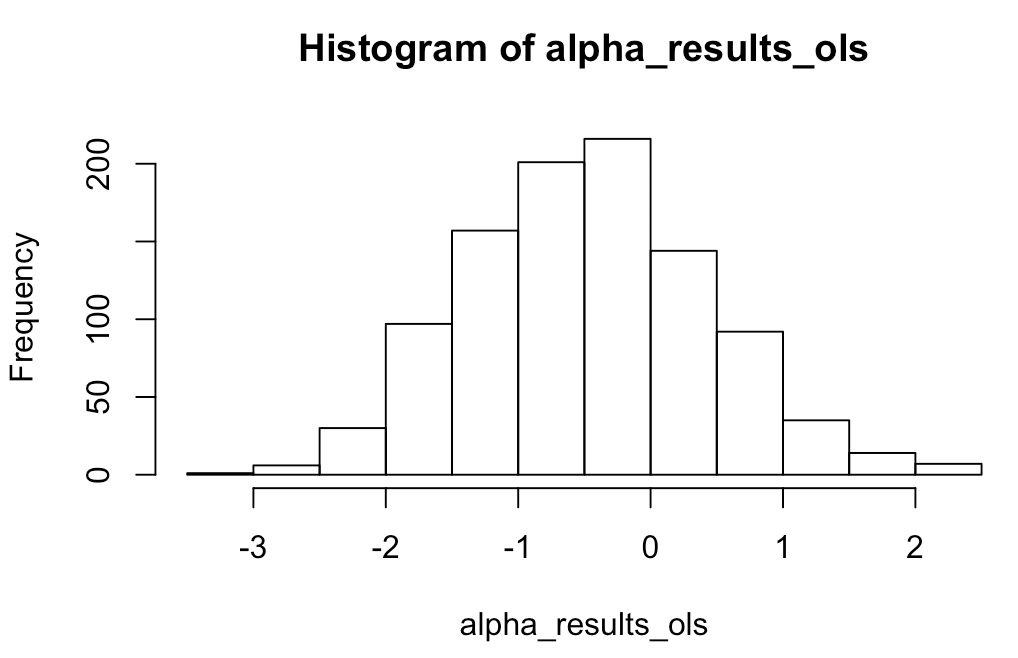
αもβも真の値（それぞれ2.5、0.6）からけっこうズレていることが分かる。

二段階最小二乗法で推定してみる

次に、内生性のあるモデルでもバイアスなく推定してくてるという噂の二段階最小二乗法をやってみます。
二段階最小二乗法が何であるかはググってどこかで見てもらえればと思いますが、あるモデル式の説明変数の中にある内生変数を、「内生変数 = α + β1外生変数1 + β2外生変数2 + ε」という形の回帰分析により、「外生変数だけで完全に説明できる部分と、それ以外の誤差」に分けます。「外生変数だけで完全に説明できる部分」というのは、この回帰分析の結果得られるαとβを用いた「予測値」のことで、内生変数のかわりにこれを使うことで、被説明変数の撹乱項と相関が生まれるのを防ぐことができるわけです。

# ========== 二段階最小二乗法で推定してみる ========== #
# さっきと同様に、αとβの真の値を設定
alpha <- 2.5
beta <- 0.6

# 推定を繰り返す関数
repeat_2sls <- function(para, n, T, sd){
  alpha_output_2sls <- c()
  beta_output_2sls <- c()
  
  # n回繰り返させる
  for (i in 1:n) {

    # 投資Itは1から始まって毎期0.5ずつ増えることにする。全部でT期分。
    It <- seq(from=1, by=0.5, length.out=T)
    
    # 変形後の上式からYtをつくる。撹乱項utは正規乱数。
    set.seed(i)
    ut <- rnorm(n=T, mean=0, sd=sd)
    Yt <- (alpha/(1-beta)) + (It/(1-beta)) + (ut/(1-beta))
    
    # Ctをつくる
    Ct <- alpha + beta*Yt + ut
    
    # ここから二段階の推定を行う。
    # まず、Y~Iの回帰分析をOLSでやります。
    model_yi <- lm(Yt ~ It)
    
    # パラメータの推定値を取り出します
    const_yi <- model_yi$coefficients[1]
    coef_yi <- model_yi$coefficients[2]
    
    # 上記パラメータからYの予測値を作ります
    Yt_pred <- const_yi + coef_yi*It
    
    # ちなみにこれは、predict関数を使って
    # Yt_pred <- predict(model_yi)
    # としても同じものが得られます。
    
    # 上の予測値を使って、二段階目の回帰をします。
    model_cy_2sls <- lm(Ct ~ Yt_pred)
    
    # パラメータの推定値を取り出します
    alpha_est_2sls <- model_cy_2sls$coefficients[1]
    beta_est_2sls <- model_cy_2sls$coefficients[2]
    
    alpha_output_2sls <- c(alpha_output_2sls, alpha_est_2sls)
    beta_output_2sls <- c(beta_output_2sls, beta_est_2sls)
  }
  
  # 出力
  if(para=='alpha'){
    return(alpha_output_2sls)
    }
  if(para=='beta'){
    return(beta_output_2sls)
    }
}

# 1000回推定して結果を取り出す。
alpha_result_2sls <- repeat_2sls(para='alpha', n=1000, T=100, sd=5)
beta_result_2sls <- repeat_2sls(para='beta', n=1000, T=100, sd=5)

# 推定値の平均を確認
mean(alpha_result_2sls)
mean(beta_result_2sls)

> mean(alpha_result_2sls)
[1] 2.524852
> mean(beta_result_2sls)
[1] 0.5996154

# ヒストグラムをかいてみる
hist(alpha_result_2sls, breaks=20)
hist(beta_result_2sls, breaks=20)

かなり「真の値」（α=2.5、β=0.6）に近い結果きました。

上記2つの計算方法の結果を比較

sd（撹乱校の標準偏差＝ばらつき）を変えてみて、両者の結果を比較します。

> # OLSでsdを1〜10まで変えてβを推定してみる
> for(i in 1:10){
+ b <- mean(repeat_ols(para='beta', n=1000, T=100, sd=i))
+ print(b)
+ }
[1] 0.6018791
[1] 0.6073759
[1] 0.6162016
[1] 0.6279157
[1] 0.6419773
[1] 0.6578006
[1] 0.6748069
[1] 0.6924639
[1] 0.7103121
[1] 0.7279768
> 
> # 2SLSでsdを1〜10まで変えてβを推定してみる
> for(i in 1:10){
+   b <- mean(repeat_2sls(para='beta', n=1000, T=100, sd=i))
+   print(b)
+ }
[1] 0.6000004
[1] 0.5999623
[1] 0.5998856
[1] 0.59977
[1] 0.5996154
[1] 0.5994214
[1] 0.5991876
[1] 0.5989136
[1] 0.5985988
[1] 0.5982427

OLSの推定のほうは、撹乱項の標準偏差を大きくしていくにつれ、推定のバイアスもどんどん大きくなってますが、2SLSのほうは結果が安定してますね。

2SLSの部分にパッケージをつかってみる

二段階最小二乗法は、semパッケージのtsls関数で簡単に実行できるので、それを使うように書き換えたものも置いておきます。

# パッケージの読み込み
library(sem)

# αとβの真の値を設定
alpha <- 2.5
beta <- 0.6

# 推定を繰り返す関数
repeat_2sls_sem <- function(para, n, T, sd){
  alpha_output_2sls_sem <- c()
  beta_output_2sls_sem <- c()
  
  # n回繰り返させる
  for (i in 1:n) {

        # 投資Itは1から始まって毎期0.5ずつ増えることにする。全部でT期分。
    It <- seq(from=1, by=0.5, length.out=T)
    
    # 変形後の上式からYtをつくる。撹乱項utは正規乱数。
    set.seed(i)
    ut <- rnorm(n=T, mean=0, sd=sd)
    Yt <- (alpha/(1-beta)) + (It/(1-beta)) + (ut/(1-beta))
    
    # Ctをつくる
    Ct <- alpha + beta*Yt + ut
    
    # tsls関数で2SLS（カンタン!!）
    model_tsls_sem <- tsls(Ct ~ Yt,  ~ It, data=data.frame(It, ut, Yt, Ct))
    
    alpha_est_2sls_sem <- model_tsls_sem$coefficients[1]
    beta_est_2sls_sem <- model_tsls_sem$coefficients[2]
    
    alpha_output_2sls_sem <- c(alpha_output_2sls_sem, alpha_est_2sls_sem)
    beta_output_2sls_sem <- c(beta_output_2sls_sem, beta_est_2sls_sem)
  }
  
  # 出力
  if(para=='alpha'){
    return(alpha_output_2sls_sem)
    }
  if(para=='beta'){
    return(beta_output_2sls_sem)
    }
}

# 1000回推定して結果を取り出す。
alpha_results_2sls_sem <- repeat_2sls_sem(para='alpha', n=1000, T=100, sd=5)
beta_results_2sls_sem <- repeat_2sls_sem(para='beta', n=1000, T=100, sd=5)


# 推定値の平均を確認
mean(alpha_results_2sls_sem)
mean(beta_results_2sls_sem)

# ヒストグラムをかいてみる
hist(alpha_results_2sls_sem, breaks=20)
hist(beta_results_2sls_sem, breaks=20)

# 2SLSでsdを1〜10まで変えてβを推定してみる
for(i in 1:10){
  b <- mean(repeat_2sls_sem(para='beta', n=1000, T=100, sd=i))
  print(b)
}

結果はさっきと同じになります（乱数のシードも揃えてるので）ので省略します。

IS-LM分析

教科書に沿って、IS-LM分析を行います。
データは、教科書のサポートサイトにあるものを使います。
https://www.nippyo.co.jp/shop/download/35.html
このデータの、islm.gdtというデータを、gretlで開いてCSVでエクスポートしておけば、Rでインポートして使えます。

IS方程式は、
lnGDPN <- α1 + β11INT + β12lnINV + u1

LM方程式は、
INT <- α2 + β21GDPN + β22lnM2CDN + u2

ここで、
GDPNは名目GDP、
INVは名目投資（民間設備投資、民間住宅投資、在庫投資の合計）、
INTは名目長期金利、
M2CDNはマネーストック
であり、lnは対数値です。

サポートサイトのデータは、1980年から2009年の日本の時系列データになっていて、変数名が、lnGDPNは「l_GDPN」、lnINVは「l_I」、lnM2CDNは「l_M2CD」になっています。

# ========== ISLM分析を二段階最小二乗法でやってみる ========== #
# パッケージの読み込み
library(sem)

# データの読み込み
data <- read.csv('data/csv/islm.csv', header=T)  # データの置き場所は各自の環境に合わせて

# IS方程式を求めるための二段階最小二乗法
tsls(data$l_GDPN ~ data$INT + data$l_I, ~ data$l_M2CD + data$l_I, data=data)

# ばらして二段階それぞれを計算しても同じ値になる
model_int_m2 <- lm(data$INT ~ data$l_M2CD + data$l_I)
INT_pred <- predict(model_int_m2)
model_gdp <- lm(data$l_GDPN ~ INT_pred + data$l_I)

model_gdp$coefficients[1]  # α1
model_gdp$coefficients[2]  # β11
model_gdp$coefficients[3]  # β12


# LM方程式を求めるための二段階最小
tsls(data$INT ~ data$l_GDPN + data$l_M2CD, ~ data$l_M2CD + data$l_I, data=data)

# ばらして二段階それぞれを計算しても同じ値になる
model_gdp_m2 <- lm(data$l_GDPN ~ data$l_M2CD + data$l_I)
GDP_pred <- predict(model_gdp_m2)
model_int <- lm(data$INT ~ GDP_pred + data$l_M2CD)

model_int$coefficients[1]  # α2
model_int$coefficients[2]  # β21
model_int$coefficients[3]  # β22

出力結果は下に貼り付けます。

> tsls(data$l_GDPN ~ data$INT + data$l_I, ~ data$l_M2CD + data$l_I, data=data)

Model Formula: data$l_GDPN ~ data$INT + data$l_I

Instruments: ~data$l_M2CD + data$l_I

Coefficients:
(Intercept)    data$INT    data$l_I 
 6.40360864 -0.05130671  0.59363934 

> tsls(data$INT ~ data$l_GDPN + data$l_M2CD, ~ data$l_M2CD + data$l_I, data=data)

Model Formula: data$INT ~ data$l_GDPN + data$l_M2CD

Instruments: ~data$l_M2CD + data$l_I

Coefficients:
(Intercept) data$l_GDPN data$l_M2CD 
   26.97856    14.70982   -13.88998 

ちなみに教科書の本文では、「二段階最小二乗法で推定された、IS方程式の利子率INTのパラメータは6.403」と書いてありますが、これは見るところを間違ってますね（定数項を報告してしまっている）。正しくは「-0.051」です。LM方程式のほうも記述が間違っています。
（出力自体は、上記の結果と教科書に載っているgretlの結果は一致しています。）

OLSでも推定してみて、ズレがどれぐらいあるか確認しておきましょう。

> # OLSでも推定してみて違いを検証
> lm(data$l_GDPN ~ data$INT + data$l_I)

Call:
lm(formula = data$l_GDPN ~ data$INT + data$l_I)

Coefficients:
(Intercept)     data$INT     data$l_I  
    5.95760     -0.04657      0.63120  

> lm(data$INT ~ data$l_GDPN + data$l_M2CD)

Call:
lm(formula = data$INT ~ data$l_GDPN + data$l_M2CD)

Coefficients:
(Intercept)  data$l_GDPN  data$l_M2CD  
     80.019        3.020       -7.491  

IS方程式のほうはある程度近い値ですが、LM方程式はだいぶ違いますね。