先日、『gretlで計量経済分析』という本に載っている二段階最小二乗法の演習をRでやってみるエントリ(リンク)を書いたのですが、同じ本の次の章は「マクロ計量モデル入門」となっていて、1980年から2009年までの日本経済のデータを用い、5本の構造方程式と2本の定義式、7つの内生変数と9つの外生変数からなる超小型のマクロ計量モデルをつくるというものでした。
Rで連立方程式を解く方法の確認がてら、Rで実行してみます。
最近、研究室の学生にRの使い方をイチから教えてるのですが、これをさらに単純化して練習問題に使えるかも……?
データは本のサポートページからダウンロードできるものですが、「model.gdt」というファイルをgretlで読み込んでcsvで書き出したものを、Rに読み込ませて使いました。
準備
データは↓のようなイメージです(画像は一部です)。
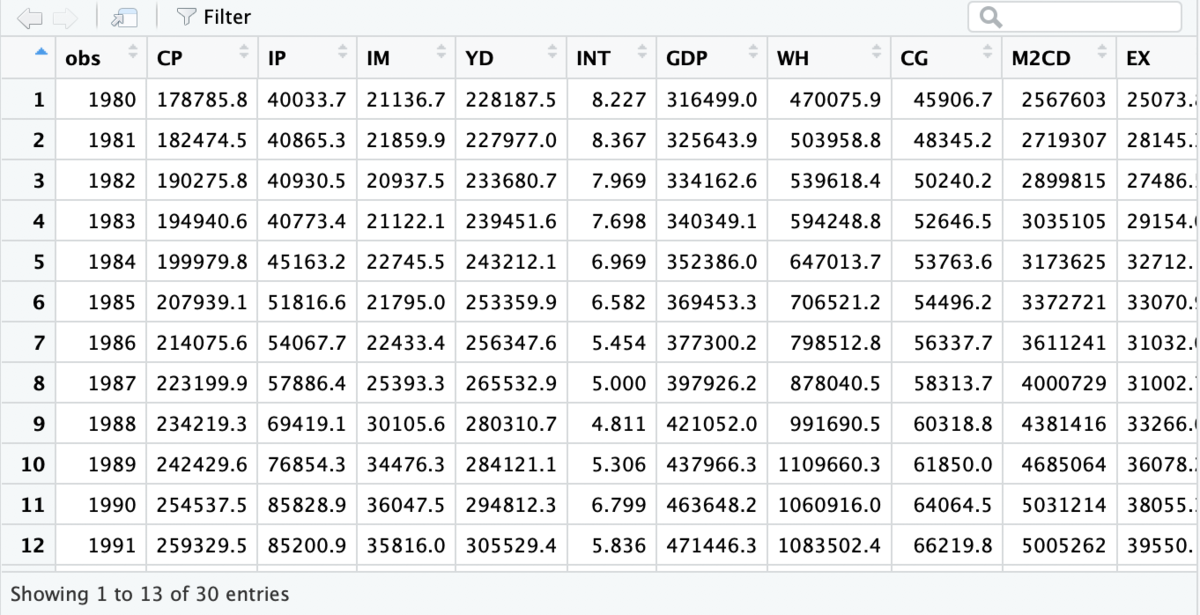
library(lmtest) library(car) library(nleqslv) # パラメータ推定用データを読み込みます d_macro <- read.csv('data/csv/model.csv', header=T) # obsという最初の列の列名称を、なんとなく、YEARに変更しておきます colnames(d_macro)[1] <- "YEAR"
元データは1980年から2009年までの日本のマクロ経済のデータですが、最大で「2期前」を取るラグ変数があることから、教科書では全て「1982年以降」のデータでパラメータを推定しているので、ここで1、2行目はカットしておきます。
d_macro <- d_macro[3:30,]
構造方程式(推計式)群のパラメータ推定
この章では、著者によると「内生性が顕著でなく、結果があまり違わないので、全て2SLSではなくOLSで推定する」とのことなので、それに合わせます。二段階最小二乗法にするなら先日のエントリの方法になりますが、そんなに手間は変わらないです。
内生変数になる「民間最終消費支出」「民間企業設備投資」「輸入」「民間可処分所得」「利子率」を推計する回帰モデルを作っていきます。
モデルの説明もコメントで書いておきますが、たとえば民間最終消費支出は、
### (1)民間最終消費支出 # CP = α + β1*YD_1 + β2*WH_1 # CP: 民間最終消費支出 # YD_1: 1期前の民間可処分所得 # WH_1: 1期前の家計金融資産残高 # 回帰分析でパラメータを推定 est1 <- lm(data=d_macro, formula=CP~YD_1 + WH_1)
こういうふうになります。
推定はもうこれでできているんですが、あとで連立方程式を解く処理のところで使いやすいように、predict()をラップして「説明変数を与えると、予測値(理論値)を吐き出す」ようにしておきます。
CP_fn <- function(YD_1, WH_1){ YD_1 <- as.numeric(YD_1); WH_1 <- as.numeric(WH_1) prd <- predict(est1,data.frame(YD_1=YD_1, WH_1=WH_1)) return(prd) }
as.numeric()しているのは、事情があります。後でここには、外生変数をまとめたデータフレームから特定の行を抜き出したあとに列名称で値を探して入れることにしたのですが、データフレームの列名称を要素名として持ったままの数字を引っ張ってくると、ここでdata.frame()内での列名称指定が無視されてしまいました。
なので、ごちゃごちゃするけどas.numeric()を挟むことにしました。
なお、predict()関数には、newdataという引数にデータフレーム型でデータを与える必要があります。
他の変数についても同じようにやっていきます。
### (2)民間企業設備投資 # IP = α + β1*(GDP_1-GDP_2) + β2*INT_l1 + β3*IP_1 # IP, IP_1: 当期と1期前の民間企業設備投資 # GDP_1, GDP_2: 1期前と2期前の実質GDP # INT: 利子率 est2 <- lm(data=d_macro, formula=IP ~ dGDP12 + INT_1 + IP_1) IP_fn <- function(GDP_1, GDP_2, INT_1, IP_1){ # 引き算は中で計算する GDP_1 <- as.numeric(GDP_1); GDP_2 <- as.numeric(GDP_2) INT_1 <- as.numeric(INT_1); IP_1 <- as.numeric(IP_1) prd <- predict(est2,data.frame(dGDP12=(GDP_1-GDP_2), INT_1=INT_1, IP_1=IP_1)) return(prd) } ### (3)輸入 # IM = α + β1*IM_1 + β2*GDP # IM, IM_1: 当期と1期前の輸入 est3 <- lm(data=d_macro, formula=IM ~ IM_1 + GDP) IM_fn <- function(IM_1, GDP){ IM_1 <- as.numeric(IM_1); GDP <- as.numeric(GDP) prd <- predict(est3,data.frame(IM_1=IM_1, GDP=GDP)) return(prd) } ### (4)民間可処分所得 # YD = α + β1*(GDP-TAX) # TAX: 租税 GDPTAX <- d_macro$GDP - d_macro$TAX est4 <- lm(data=d_macro, formula=YD ~ GDPTAX) YD_fn <- function(GDP, TAX){ # 引き算は中で計算する GDP <- as.numeric(GDP); TAX <- as.numeric(TAX) prd <- predict(est4, data.frame(GDPTAX=(GDP-TAX))) return(prd) } ### (5)利子率(LM方程式) # INT = α + β1*ln(GDP) + β2*ln(M2CDN) # M2CDN: マネーストック est5 <- lm(data=d_macro, formula=INT ~ l_GDP + l_M2CDN) INT_fn <- function(GDP, M2CDN){ # 対数化は中で GDP <- as.numeric(GDP); M2CDN <- as.numeric(M2CDN) prd <- predict(est5, data.frame(l_GDP=log(GDP), l_M2CDN=log(M2CDN))) return(prd) }
ところで、5番目の利子率の式は、教科書とはやり方を変えています。
GDPも内生変数なので、ln(GDP)で説明されるINTはGDPと同時に決まるという構造ですが、gretlでは連立方程式を解かせるときに、「内生変数として計算されたGDPのlogを取って、別の内生変数の説明変数にする」という処理が書けない(?)らしいので、教科書ではちょっと変なやり方で代用していました。
どういうやり方かというと、推定用元データ上は、ln(GDP)はエクセルか何かで予め計算してあって、元データのテーブルに一つの変数として入っているのですが、その上でまず、
ln(GDP)〜GDP
という回帰分析を行っています。(つまり、対数を取る処理を線形モデルで代用している…)
この回帰分析の結果を使って、GDPをln(GDP)ではない何かに変形したものを、疑似ln(GDP)としてINTの説明変数に入れているわけです。
しかしここではそんなことはせずに、普通に、GDPのlogをとってそれをINTの予測に用いるようにしておきます。
なので、教科書とは、最終の結果が少しずれます。(ここを教科書どおりにすると最終結果がピッタリ一致することは確認しました。)
lmの結果をまとめてCSV出力する
べつにやる必要はないのですが、上の回帰分析の結果をまとめて表にして出力する関数も書いておきます。
# 関数定義 save_lm_results <- function(model, model_name='none'){ sum <- summary(model) coef <- sum$coefficients R2 <- c(sum$r.squared, NA, NA, NA) Adj_R2 <- c(sum$adj.r.squared, NA, NA, NA) # ダービンワトソン検定(p<.05だと系列相関あり) DW_test <- c(dwtest(model)$statistic, NA, NA, dwtest(model)$p.value) # Breusch-Godfrey検定(p<.05だと系列相関あり) BG_test <- c(bgtest(model)$statistic, NA, NA, bgtest(model)$p.value) results <- rbind(coef,R2, Adj_R2, DW_test, BG_test) if(length(model$coefficients)-1 >= 2){ # 説明変数が2個以上あるならVIFを計算する VIF <- c(NA, vif(model), NA, NA, NA, NA) } else{ VIF <- c(NA, NA, NA, NA, NA, NA) } results <- cbind(results, VIF) # モデル名を指定しない場合はformulaをファイル名にする if(model_name=='none'){ output_name <- as.character(paste(model$call$formula[2], model$call$formula[1], model$call$formula[3], sep='')) } else{ output_name <- model_name } write.csv(results, paste('results/lm_result_', output_name, '.csv', sep=""), row.names=TRUE, quote=FALSE) } # 実行(空のリストがコンソール上に出力されるけど気にしない) lapply(X=list(est1, est2, est3, est4, est5), FUN=save_lm_results)
恒等式(定義式)群の定義
マクロモデル中の定義式(パラメータを推定するのではなく変数間の定義上の関係を記述するもの)を記述しておきます。
### (6)国内総生産 # GDP = CP + IP + CG + IG + IH + ST + EX - IM # CG: 政府最終消費支出 # IG: 公的資本形成 # IH: 住宅投資 # ST: 在庫投資 # EX: 輸出 GDP_fn <- function(CP, IP, CG, IG, IH, ST, EX, IM){ def <- CP + IP + CG + IG + IH + ST + EX - IM return(def) } ### (7)名目国内総生産 # GDPN = GDP*GDPDEF/100 # GDPDEF: GDPデフレータ GDPN_fn <- function(GDP, GDPDEF){ def <- GDP*GDPDEF/100 return(def) }
外生変数テーブルを作る
さてここからは、推定されたパラメータをつかってシミュレーションを行っていきます。
外生変数をどうやって与えようかなと思ったのですが、なんとなく、データフレームに整理しておいて、そのうち1行を選択して与えると、全ての外生変数を読み込んで内生変数を導いてくれるような組み立てがわかりやすいかなと思い、そうしてみました。
まず、パラメータの推定に使ったデータから、外生変数として使用する変数群を抜き出してまとめます。
Exog_df <- d_macro[,c( 'YEAR', 'YD_1', 'WH_1', # CPの説明変数(他との重複は除く) 'GDP_1', 'GDP_2', 'INT_1', 'IP_1', # IPの説明変数( 〃 ) 'IM_1', # IMの説明変数( 〃 ) 'TAX', # YDの説明変数( 〃 ) 'M2CDN', # INTの説明変数( 〃 ) 'CG', 'IG', 'IH', 'ST', 'EX', # GDPの定義に使う( 〃 ) 'GDPDEF' # GDPN(名目GDP)の定義に使う( 〃 ) )] # 1982年以降のデータだけ抜き出す Exog_df <- subset(Exog_df, Exog_df$YEAR >= 1982)
上記で抜き出した外生変数のテーブルには、外生というよりも「先決内生変数」と言われるものが混じっていて、たとえば「1期前のGDP」であれば、前のサイクルで推定された内生変数であるGDPの値を、当期の外生変数のようにして使うというものです。
先決内生変数については、見間違えないように、必要なもの以外はデータをNAに置き換えておくことにします。
1期のラグ変数なら1982年だけ残し、2期のラグ変数なら1983年まで残しておく必要があります。
# NAに置き換える関数 remove_future_data <- function(df, valname, lag){ colnum <- which(colnames(df)==valname) df[(lag+1):nrow(df),colnum] <- rep(NA, (nrow(df)-lag)) return(df) } # 先決内生変数の使わない値を置き換え Exog_df <- remove_future_data(df=Exog_df, valname='IP_1', lag=1) Exog_df <- remove_future_data(df=Exog_df, valname='IM_1', lag=1) Exog_df <- remove_future_data(df=Exog_df, valname='YD_1', lag=1) Exog_df <- remove_future_data(df=Exog_df, valname='INT_1', lag=1) Exog_df <- remove_future_data(df=Exog_df, valname='GDP_1', lag=1) Exog_df <- remove_future_data(df=Exog_df, valname='GDP_2', lag=2)
内生変数の値を得る
「外生変数を与えると、連立方程式を解いて内生変数を返してくれる」という処理を書いていきます。
連立方程式を解くnleqslv()の使い方は次の通り。
未知数が並んだベクトルだけを引数に取る関数(f0とする)を定義して、nleqslv()に、関数foと「未知数の初期値ベクトル」を与えると、未知数の値をちょっとずつ変えてf0に与えながら、f0がゼロになる未知数の組み合わせを探してくれます。
つまりf0は、連立方程式が解けたらゼロベクトルになるように記述しておく必要があります。
たとえば、
INT = α + β1*ln(GDP) + β2*ln(M2CDN)
というような関係を想定しているのであれば、移項して、
INT -(α + β1*ln(GDP) + β2*ln(M2CDN))
というように記述しておくことになります。
で、以下のように定義する関数で、1期分の外生変数を与えると、その期の内生変数が得られます。
xの並び順に注意が必要です。
# 内生変数を計算する関数 get_endo <- function(init, exo, year){ e <- subset(exo, exo$YEAR==year) fn0 <- function(x){ # xはCP,IP,IM,YD,INT,GDP,GDPNの順 output <- c( x[1] - CP_fn(e$YD_1, e$WH_1), # CP=の方程式 x[2] - IP_fn(e$GDP_1, e$GDP_2, e$INT_1, e$IP_1), # IP=の方程式 x[3] - IM_fn(e$IM_1, x[6]), # IM=の方程式 x[4] - YD_fn(x[6], e$TAX), # YD=の方程式 x[5] - INT_fn(x[6], e$M2CDN), # INT=の方程式 x[6] - GDP_fn(x[1], x[2], e$CG, e$IG, e$IH, e$ST, e$EX, x[3]), # GDP=の方程式 x[7] - GDPN_fn(x[6], e$GDPDEF) # GDPN=の方程式 ) return(output) } solution <- nleqslv(x=init, fn=fn0, method = "Newton") return(solution$x) }
内生変数を保存するテーブルを作っておきます。
Endog_df <- data.frame(YEAR = Exog_df$YEAR, CP = rep(NA, nrow(Exog_df)), IP = rep(NA, nrow(Exog_df)), IM = rep(NA, nrow(Exog_df)), YD = rep(NA, nrow(Exog_df)), INT = rep(NA, nrow(Exog_df)), GDP = rep(NA, nrow(Exog_df)), GDPN = rep(NA, nrow(Exog_df)) )
次に、先ほど定義した関数を繰り返し使って各期の内生変数を順次求めていき、外生変数テーブルと内生変数テーブルをともに1期ずつ更新していく関数を書いておきます。
simulate <- function(init, exo_df, endo_df){ for (i in 1:nrow(exo_df)){ # iサイクル目の外生変数セット(1行だけのデータフレームの形) exo <- exo_df[i,] # iサイクル目の解を求める sol <- get_endo(init=init, exo=exo_df, year=exo_df$YEAR[i]) # 内生変数テーブルのi行目を更新 endo_df[i,'CP'] <- sol[1] endo_df[i,'IP'] <- sol[2] endo_df[i,'IM'] <- sol[3] endo_df[i,'YD'] <- sol[4] endo_df[i,'INT'] <- sol[5] endo_df[i,'GDP'] <- sol[6] endo_df[i,'GDPN'] <- sol[7] # 得られた内生変数を、外生変数テーブルのy+1年の行に先決内生変数 # として上書きする(ただしiが終わりの年を超えるまで) if(i<nrow(exo_df)){ exo_df[i+1,'IP_1'] <- sol[2] exo_df[i+1,'IM_1'] <- sol[3] exo_df[i+1,'YD_1'] <- sol[4] exo_df[i+1,'INT_1'] <- sol[5] exo_df[i+1,'GDP_1'] <- sol[6] # 2サイクル目からはGDP_2(の3行目以降)も更新する if(i>=2){ exo_df[i+1,'GDP_2'] <- endo_df[(i-1),'GDP'] } } } output <- list(endo_df, exo_df) return(output) }
ではいよいよ下記でシミュレーションを実行します。
内生変数の初期値は、全部0とかにしててもきちんと推計できましたが、推計に使った元データの平均値を取って入れるようにしておきます。
# 内生変数の初期値(元データの平均) initial <- c(mean(d_macro$CP), mean(d_macro$IP), mean(d_macro$IM), mean(d_macro$YD), mean(d_macro$INT), mean(d_macro$GDP), mean(d_macro$GDPN)) # シミュレーション実行 results <- simulate(init=initial, exo_df=Exog_df, endo_df=Endog_df) # 結果の取り出し Endo_results <- results[[1]] Exo_results <- results[[2]] # 結果の保存 write.csv(Endo_results, 'results/Endo_results.csv', quote=FALSE, row.names=FALSE) write.csv(Exo_results, 'results/Exo_results.csv', quote=FALSE, row.names=FALSE)
得られた結果を推計に使った元データと比較してみます。
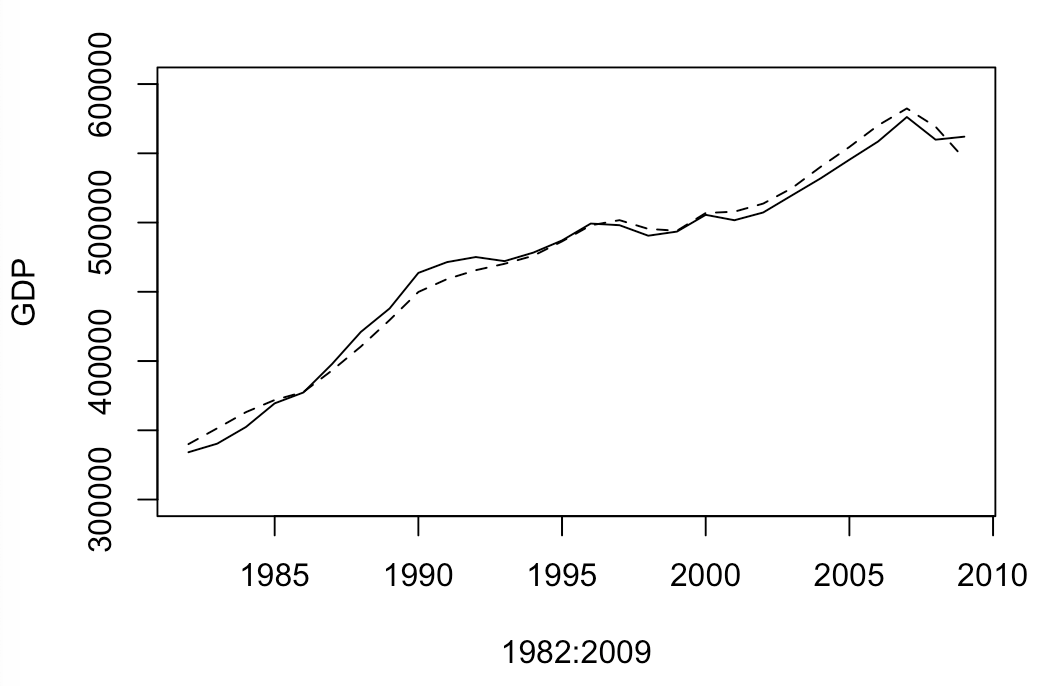
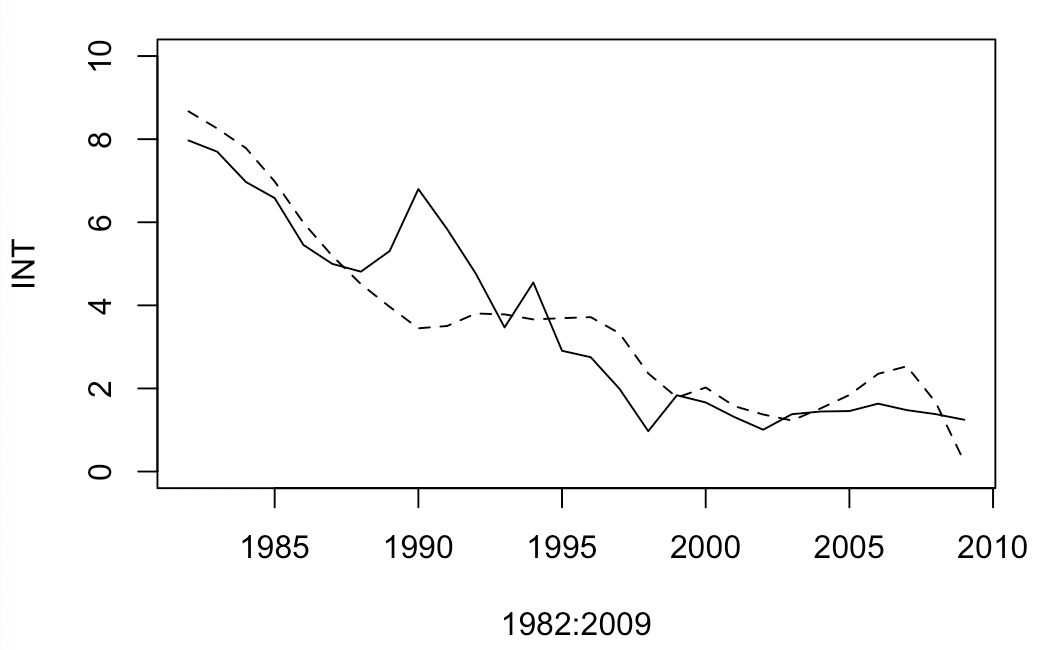
GDPとINT(利子率)の予測値と実績値を並べておきます。実線が実績値、破線が予測値(シミュレーション値)です。
xlim=c(1982,2009) ylim=c(300000, 600000) plot(x=1982:2009, d_macro$GDP, type='l', lty=1, xlim=xlim, ylim=ylim, ylab="GDP") par(new=TRUE) plot(x=1982:2009, Endo_results$GDP, type='l', lty=2, xlim=xlim, ylim=ylim, axes = FALSE, xlab="", ylab="") xlim=c(1982,2009) ylim=c(0, 10) plot(x=1982:2009, d_macro$INT, type='l', lty=1, xlim=xlim, ylim=ylim, ylab="INT") par(new=TRUE) plot(x=1982:2009, Endo_results$INT, type='l', lty=2, xlim=xlim, ylim=ylim, axes = FALSE, xlab="", ylab="")
教科書に従ってOLSで推定しましたが、2SLSにしても大して手間はかからないと思います。