血液型と性格の関係
産経新聞のネット記事で、首相の血液型はO型が多いということや、増税する首相はB型が多いといったことが書かれていました。
この一覧表をみてみると、興味深いことがいくつか浮かび上がってきました。
1つは、O型が突出して多いということです。36人中18人と実に半数を占めており、次いでA型の10人、B型の5人、AB型の2人(小磯国昭は不明とされていました)。
日赤などの資料による日本人の割合(A型は4割、B型は2割、O型は3割、AB型は1割)と比べてみると、歴代首相のデータには偏りがあるのがわかります。
【政治デスクノート】「増税」と「首相の血液型」の仰天関係… 財務省“極秘資料”は雄弁に語っていた(1/4ページ) - 産経ニュース
私は、血液型性格占いが科学的にはまったく支持されていないというのは知ってますが*1、個人的には関連性があったほうが面白いと思っていて、血液型の話は好きです。
上記記事のブコメをみると「エセ科学」とかいって叩かれてましたが、そもそもネタ記事なんだから良いじゃん……と思いましたね。血液型性格診断って、「科学的には支持されてないらしい」ということ自体がよく知られていて話題になりやすいので、私が飲み会とかで血液型の話をしたときも「いやいやそれって心理学者とかが実験してて否定されてんだよ」とドヤ顔で突っ込んでくる人がたくさんいますね。なぜか荒れやすいネタのようです。
で、ブコメをみてたら「サンプル少なすぎだろ。」というコメントがありました。その点は気になったので、とりあえず「日本人の平均に比べて首相はO型が多いかどうか」をRで仮説検定してみました。
一応断っておくと、実際に記事の仮説が正しいかどうかを知りたいというよりは、単に統計の勉強がてらやってみたというものです。母集団における比率の想定が30%で、36人の標本中の比率が50%ってのは、偏りがあることをどれぐらい主張できるんだろうか、と。
なお、何しろ私は初学者ですので、間違ってるかもしれません。しかも今仕事で外出してて、飯田橋の喫茶店で休憩時間中に書いているので、あまり考える時間もありませんw
間違いがあれば指摘していただけるとたいへん助かります……。
「増税する首相はB型だ」というのについては、これより難しそうなのと、時間もないのでやめときます。A:O:B:ABの全体の比率の検定は、「追記2」で触れているとおり、期待度数が小さすぎるセルがあってダメでした。
Rで検定してみる
さて、記事によれば、東条英機以降の首相36人中18人がO型であるが、日本人全体のO型率は3割とされています。
日本人のA、O、B、ABの割合が4:3:2:1になるというのは、血液型性格診断のファンならば当然知っている数字ですね!!*2
仮に首相のO型率が日本人の全体と同じ「3割」であるというのが真実であると仮定して(帰無仮説)、今回の「36人中18人」という数字が、統計的に有意に「3割」から乖離してると言えるかどうかを検定することが考えられますね。有意に乖離してるなら、3割とは言えないということになります。
まぁ、血液型と関係あるのかを本当に知りたくて分析しようと思ったら、岸首相と安倍首相みたいに血のつながりがある場合は……とか考えないといけないのですが、単に仮説検定の勉強なので、この36人には「首相である」という以外にとくに情報がないことにしましょう。
比率がある特定の値であると言えるかどうかの検定は、たとえばその乖離をZ値に変換することで行うものがある。
比率の検定・独立性の検定
↑のページの「1母比率の検定」のところで定義されている検定統計量Zが標準正規分布に従うという性質を利用すれば行えるとのことだ。
(他にもいろいろな検定方法があるみたい。)
は標本の比率で、
は母集団の比率で、
は標本サイズです。
ではZ値をRで計算してみます。
> Z.value <- function (prop, n, prop0) { + #propが標本の比率 + #nが標本数 + #Prop0が母集団比率 + #propのほうがprop0より大きい場合にZが正になる + (prop - prop0) / sqrt(prop0*(1-prop0)/n) + } > > Z <- Z.value(0.5, 36, 0.3) > print(Z) [1] 2.618615
2.62と出ました。
標準正規分布表をみると、0から2.62という値までの確率は0.4956であり、逆にいうと2.62以上になる確率は、0.5から引くので、0.0044ぐらいしかないことになります。両側で検定するとしてもp値が0.009弱ぐらいになるので、1%水準で有意ということになりました。
「首相の真のO型率」が日本人全体と同じく3割だった場合、36人の首相のうち18人がたまたまO型になる確率は、1%もないということです。(正確にいうと、18人以上になる確率が0.44%未満ということ。)
つまり、首相36人中18人(5割)がO型であるというのは、「日本人全体の3割がO型」という比率からすると、たまたま偶然多かったとは言えず、首相はO型が多いといえるっぽい。
標準正規分布表をみなくても、積分すれば確率は計算できますね。
> # Zが上記のような値以上になる確率を求めてみる > # 単に標準正規分布の確率密度関数を、0〜Zまで積分すると片側の確率が出る > int <- integrate(dnorm, 0, Z) #dnormはデフォルト設定だと標準正規分布になる > p <- 2 * (0.5 - as.numeric(int[1])) #数字に変換する必要があったので > print(p) [1] 0.008828761
0.0088らしいです。
なんか、integrate()したら値がリストの第1要素として返されたので(そういうもん?)、数字に変換しておきました。
0~Zまでの確率密度を積分して0.5(片側なので)から引いていますが、ZからInf(無限大)までの積分でもいいとおもいます。
関数があるらしい
ところで、↓のページをみると、Rで母集団比率の検定をしたいときは、prop.test()関数かbinom.test()関数を使えばいいらしいです。
ヒストグラムと密度曲線
前者は中身がどういう計算なのかは分かってませんが、後者は二項検定ってやつですね。
上記ページでは、prop.test関数の使い方が書かれているのでやってみます。
> prop.test(x=18, n=36, p=0.3, alternative ="two.sided", conf.level = 0.95) 1-sample proportions test with continuity correction data: 18 out of 36, null probability 0.3 X-squared = 5.9378, df = 1, p-value = 0.01482 alternative hypothesis: true p is not equal to 0.3 95 percent confidence interval: 0.3322476 0.6677524 sample estimates: p 0.5
p-valueが0.01482なので、帰無仮説は5%水準で棄却される。つまり母比率(首相のO型率の真の値)は、0.3ではなさそうだということです。
さっきのZ値による検定と結果が少し違いますが、使い分けの条件とかは分かってないのであとで勉強しとかないと……。
当然ですが95%信頼区間をみても、0.3という値は含まれてないので、この標本からは「首相のO型率の真の値」が0.3といえる可能性は低いことになりますね。
言い換えると、東条英機以降の首相のO型率は、日本人の平均よりも多いと言えます。。。
ちなみに、Rの関数マニュアルをみると、p.62に、prop.test()の使い方が書いてあります。binom.test()の使い方はp.53に載っていますね。
二項検定のbinom.test()もつかってみると、
> binom.test(18,36,p=0.3) Exact binomial test data: 18 and 36 number of successes = 18, number of trials = 36, p-value = 0.01639 alternative hypothesis: true probability of success is not equal to 0.3 95 percent confidence interval: 0.3292218 0.6707782 sample estimates: probability of success 0.5
似たような結果になりました。
間違ってたらすいません。ご指摘いただければありがたいです。
ちなみに、私はB型です。
(追記1)乱数で実験してみる
直観的には、36人しかいないんだからそのうち18人がO型になる程度のブレは、あって当たり前じゃんって思ってしまう(冒頭で言及したブコメが言うように)ので、乱数を使って実験してみました。
1億2000万人のうち、4割がA型、3割がO型、2割がB型、1割がAB型になるようなデータをつくり、36人を無作為抽出したときに、O型が何人含まれているのかを数えます。
1万回サンプリングしてみて、O型の人数がどのようにばらつくかをみてみます。
# A型が4800万人、B型が2400万人、C型が3600万人、AB型が1200万人となるデータをつくる d <- c(rep("A", 48000000), rep("B", 24000000), rep("O", 36000000), rep("AB", 12000000)) # 36人をランダムサンプリングして、O型の人数を数えて記録するという作業を1万回繰り返す Os <- c() for (i in 1:10000) { s <- sample(d, 36) Os <- c(Os, length(which(s=="O"))) } > length(which(Os >= 18)) / 10000 # 18以上になる割合 [1] 0.0083
36人を無作為抽出してO型が18人以上になった割合は、1%未満でした。
最初のZ値での検定と違って片側(0.3より大きいほうへの乖離)しか見ていない点に注意が必要です。0.3より大きいか小さいか、予め想定する根拠は無いように思いますので、両側検定の考え方でみるとすると、prop.test()とかの結果に近い気がします。
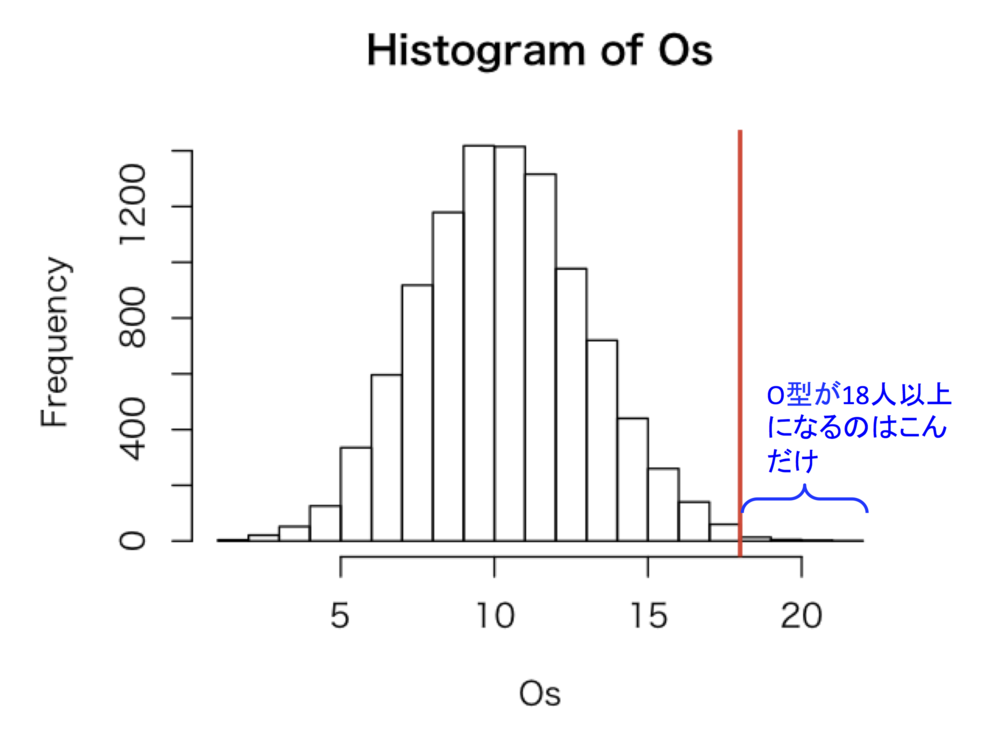
一応、グラフも貼っておきますが、完全にランダムな抽出の場合に、母集団比率が30%なのに36個の標本中の比率が50%になるってのはかなり稀なこと(つまり36人の首相の血液型には本当に偏りがある可能性が高い)ってことが分かります。
> hist(Os) > abline(v=18, col="red", lwd=2)
(追記2)適合度検定
よく考えたら、上記のようにO型の割合だけを見ているのは問題があるかもしれず、A型:O型:B型:AB型の割合が首相においては10:18:5:2であるという全体の組み合わせを検定してみる必要もあります。
↓のページにまさに血液型の例で、標本の分布が理論分布から乖離しているかどうかをカイ二乗検定で確かめている例が載っています。
Rでの実行の仕方は↓に書いてあり、引数として、標本分布のベクトルと、その理論分布を確率で表したベクトルを与えてやればいいらしい。引数「p=」には確率を与えるので、ここは足して1になるようにしするわけです。
実際に検定してみると、
> chisq.test(c(10,18,5,2), p=c(0.4,0.3,0.2,0.1)) Chi-squared test for given probabilities data: c(10, 18, 5, 2) X-squared = 7.7143, df = 3, p-value = 0.0523 Warning message: In chisq.test(c(10, 18, 5, 2), p = c(0.4, 0.3, 0.2, 0.1)) : Chi-squared approximation may be incorrect
p値が0.0523なので有意ではないという結果になるのですが、上記のようにWarningがでます。これは度数が少なすぎるということですね。
カイ二乗検定では、期待度数が5未満のセルがあってはならないこととされており、先ほどみた「カイ2乗分布,カイ2乗検定」のページでも、期待度数が小さいセルができてしまうときはセルを併合することで、つまり分類を大ざっぱにすることで解決しろと書いてありますね。
2×2分割表で独立性の検定をやるときは、こういう場合fisher.test()でフィッシャーの正確確率検定をやれということになってるのですが、理論的な理解をしていないため、今回のようなケースでどう対処していいかは私には分かりません。。。
ひとまずこういう結果である以上、36人程度のサンプルでは、A:B:O:ABにまで細分化したカイ二乗検定は行ってもあまり意味がないということになるんじゃないでしょうか。なのでこのエントリの前半で行ったように、「O型の割合は有意に多い」という程度のことを言うに留めておいたほうが無難な気がします。
ただし、「血液型と性格に関連はあるのか ― 適合度検定,2標本検定」という資料でも書かれているように、サンプルサイズが大きければ良いというもんでもないと思いますが。
あと、分散分析で多重比較をやるときに似た問題もあるのかな?つまり、全体としては理論分布から有意に乖離しているとは言えないのに、個別項目ごとに比較する場合には、項目数が多くなればなるほど「1組ぐらいは有意差が出てもおかしくない」という問題です。ただこれについては、「カイ二乗検定(独立性検定)から残差分析へ:全体から項目別への検定 - Yahoo!知恵袋」というページの一番下でも書かれているように、自分が注目している項目の差だけ見てればいい気もします。
余談になりますが、分散分析の場合でも↓のような意見をみました。
多重比較を実施して,第一種の過誤が増えないように調整をするのです.ただし,検定を繰り返しするという観点に立つなら,分散分析で主効果と交互作用の検定を同時に行うことも検定の繰り返しですし,重回帰分析で複数の独立変数の効果を見ることも検定の繰り返しです.共分散構造分析のパスの有意性検定も,複雑なモデルほど多くの検定をしています.その意味で,多群の分散分析にだけ,多重比較の問題がうるさく言われるのは,やや不思議な感もします(これは私見です)
全体としてのあてはまりをみているのか個別の項目をみているのかという、分析者の観点さえ明確であれば、べつに個別に比較しても良いような気はしますね。もともと多重比較の問題も、部分における有意差をもって全体に有意差があると勘違いしてはならないということだと思うので。
いずれにしても、カイ二乗検定の性質とか、分散分析の多重比較の問題とかは、統計の教科書では割と早い段階で出てくる基本事項である割に、イマイチきちんと頭に入ってないので、今後しっかり勉強して間違いなく使えるようにならないと……と思っております。
(追記3)血縁の問題
↓のようにコメントを頂いたとおり、有意に乖離しているとしたら、血縁ぐらいしか理由は思いつかないですねw
@KWBT_JP これが原因かも。http://t.co/DOXXnVjjeC
— 平田朋義 (@tomo3141592653) October 7, 2014