7/24(木)の勉強会では、永田・棟近『多変量解析法入門』(以下、基本的に「永田・棟近教科書」と呼ぶ。)の第9章「主成分分析」を扱いました。

- 作者: 永田靖,棟近雅彦
- 出版社/メーカー: サイエンス社
- 発売日: 2001/04
- メディア: 単行本
- 購入: 2人 クリック: 9回
- この商品を含むブログ (1件) を見る
ちなみに勉強会でこの教科書を扱うのは2回目で、1回目の範囲は「第3章 線形代数のまとめ」でした。
以下、今回の学習ノートです。なお、たいへん長くなったので、教科書に出てくる計算事例のRでの実行については、別のエントリに書きました。(この教科書自体Rとは関係ないので、計算結果の数表しか載ってないです。)
主成分分析に関するメモ
主成分分析について学んだことをカンタンにまとめていくが、まとめるのは計算手順ではなく、主成分分析の意味合いを初学者なりに理解するためのメモでである。具体的な計算方法とかをイチから解説するわけではない。なお、私は所詮初学者なので、理解の間違いとかもあるのでは……と思っています(汗
以下のまとめの前半は、主成分分析の理解そのものに関わるメモであり、永田・棟近教科書とは無関係に読んで頂ける内容である。
一方後半は、永田・棟近教科書を読み進める上で、注意点とか重要だと思った点(注釈みたいなもの)をまとめておく。なので後半については、教科書が手元にないと何のことを言ってるのかわからない内容です。
主成分分析とは
主成分分析とは、変数がたくさんあるときに、それらの変数を合成して「主成分」と呼ばれる新たな変数を作りだし、その新たな変数によって元のデータを近似することで、「より少ない変数による、シンプルな表現」を可能にする分析手法である。より次元の低いベクトル空間への、元のデータの特徴をなるべく失わないような写像を求めていると言ってもよい。
これは他の解説書や解説サイトでも同じだが、学校のテストの各科目の点数を合成して総合的な「賢さ」の指標をつくるといったケースが定番の例として紹介される。
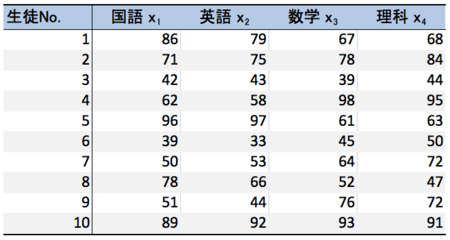
10人の生徒の、国語・英語・理科・数学の4科目の得点が与えられており、言い換えると10人の生徒の特徴が4つの変数で表現されていることになるわけである。
この10人の4変数からなる特徴を、たとえば「賢さ」という1つの変数にまで圧縮して表現しようと思ったとき、たとえば4教科の「平均点」を用いるという方法がまず考えられる。しかし単純な平均点だと、各科目の難しさが違ったりした場合に不公平になる恐れがあるので、重み付けを行ったほうがよい。主成分分析で得られる主成分とは、観測変数に重みをつけて合成することによって、
- 各観測変数をなるべく平等に反映させる
- 情報量のロスがなるべく少ない近似(各観測変数からなるべく乖離が出ない合成変数*1)になるようにする
ような手法であると言える。
「情報量のロス」という場合の情報量とは、この場合は各変数が持っている分散のことを指している。変数を標準化して計算するので全体の情報量=分散は変数の数に一致するわけだが、この意味は最初は分かりにくかった(永田・棟近教科書ではじめて出てきたわけではない)。
和歌山大の先生が主成分分析を解説したPDF資料(リンク)にも書かれているのだが、2つの変数を1つの変数に縮約することを目指す場合、たとえばx軸とy軸によって表現されていた各サンプルのデータ(1人1人の特徴みたいなもの)を、z軸1本で表現することにしたと思えば良い。
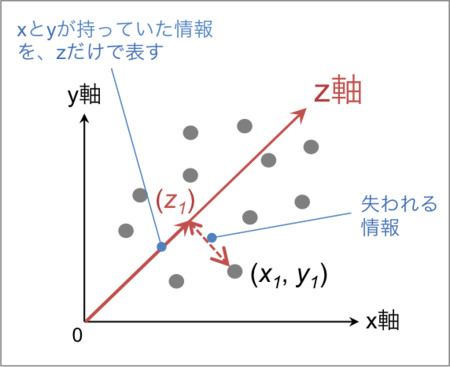
ある人の特徴がもともとという座標で表されていたのを、
だけにしてしまうわけである。
この場合、z軸の方向のばらつき=情報量はしっかり表現されるが、それと垂直方向の情報はすっぽり失われてしまう。
つまるところ「ばらつき」というのは、「各サンプル間の違い=特徴」のことである。ばらつきが「ゼロ」というのは、たとえば全員の国語のテストの点数が同じだったみたいなケースなのだが、この場合、国語の点数という情報によって生徒間の違いを議論することができない。つまり、国語の点数という変数では生徒1人1人の特徴を言い表すことが全くできないので、この変数の情報価値はゼロということになるわけである。
観測変数を適切に縮約する主成分(のモデル式)を求める手法は結果的にはカンタンで、
- 観測変数間の相関行列をつくる
- 相関行列の固有値・固有ベクトルを求める
- 各固有値に対応する固有ベクトルを係数とした主成分が求まる
- 各主成分と各観測変数の(偏)相関=因子負荷量は、固有値の平方根×固有ベクトルの要素として求めることができる
というものである。
永田・棟近教科書では、まず2変数を1変数に縮約するケースを扱い、その後に変数がp個の場合にまで拡張できることを示している。また、主成分の分散を最大化するという基準での解法の他に、主成分と観測変数の相関を最大化するという解法も存在するのだが、結果的には同じ固有値問題に帰すると説明されている。(具体的な数式の展開などの解説はない。)
主成分分析と因子分析の違い
初学者としてやはり気になるのは、主成分分析と因子分析の違いである。
観測変数のデータを、観測変数よりも少ない変数で説明しようとするところとか、その少ない変数ってのが元の観測変数に共通に影響を与えているところとかがとても似ているので、一見ごっちゃにしてしまいがちである。
だからこそ、たとえば「主成分分析は因子分析ではない!」(リンク)というような資料が存在して、「似て非なるものなのだ」ということをわざわざ解説したりする人がいるわけである。
ちなみにこの「主成分分析は因子分析ではない!」というPDF資料はとても分かりやすい。要するに主成分分析と因子分析は、目的が真逆だということである。
主成分分析というのは手元の観測データを「縮約」する、すなわちより少ない変数で近似することによって、解釈しやすくしようというものであり、主成分は観測変数の合成変数だ。
それに対して因子分析というのは、手元の観測データはまだ観測されていない「共通因子」の一つの現れであると考える。つまり共通因子(と観測変数ごとの独自性)を合成して、観測変数が生まれていると考えるわけである。
因子分析の場合は、統計ソフトで計算するときもそうだが、まず因子数を指定しないといけない。「良い感じの因子数」を仮定してみて、「良い感じに回転」(斜交回転も行う)することで、元のデータを綺麗に表現できる共通因子を求めていくわけである。
一方主成分分析の場合、主成分は、1個目からp個目*2までいっぺんに求まる。たとえば観測変数が4個あれば、それらの変数を線形結合した合成変数としての「主成分」を互いに直交するように4本作ることができ*3、これら4本の合成変数によって元の観測変数が持っている情報を完全に表現することができるのだが、この4本の式はいきなり同時に求まってしまう。で、だいたい最初の1本とか2本を用いて、情報の大半が説明できてしまうので、それ以降の主成分は無視しておこうという話になるわけである。
このことと関連するが、因子分析の場合、2因子モデルで解析した結果と3因子モデルで解析した結果は大きく異なることもしばしばだが、主成分分析の場合は1成分で表現しようが3成分で表現しようが、第1主成分、第2主成分……の内容は全く変わることがない。
また、主成分分析の場合、とくにこの教科書でも例示されているような、国語・英語・数学・理科の点数の解析みたいなケースでは、第1主成分は基本的に「総合指標」になるという点に注意が必要だ。
たとえば、4教科の点数が
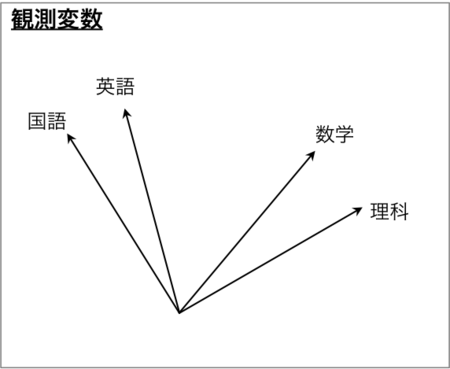
↑のようにベクトルで表現されたとする。(ほんとは、たとえばサンプル数が10あったら10次元空間上にベクトルを描かないといけないが、たまたま平面上に並んだとする。)
これを「因子分析」しようと思った場合、ふつうに考えると、
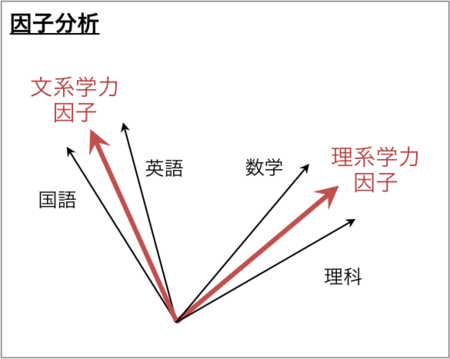
みたいな感じの2因子でしっくりくるような解釈ができるはずだと直感的に期待するし、実際分析するとそうなるだろう。
ところがこのデータを主成分分析した場合、まず第1主成分はどんな感じかというと、

↑こういうベクトルなのだ。第1主成分というのは、「1本のベクトル(主成分)で4本の観測変数ベクトル全部を効率よく近似しよう」とする変数なわけだから、当然こうなる。
そして第2主成分を求めると、第2主成分というのは第1主成分に直交するベクトルだから、たとえば、
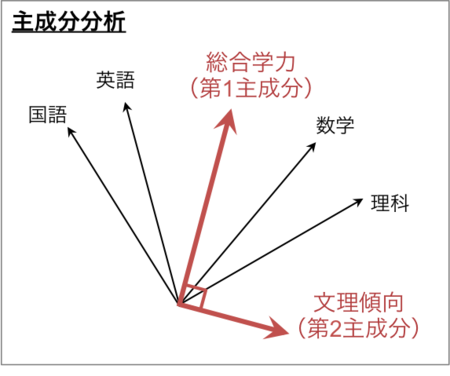
↑こんな感じになるわけである。
実際に教科書の計算例でも、4教科の点数を主成分分析にかけて求まる第1主成分は「総合的な学力」を表しており、第2主成分は「文系・理系傾向」を表していると解釈されている。つまり、まず「賢さ」という究極の総合指標を作ってみて、それでこぼれ落ちている情報量(国英⇔数理の方向のばらつき)を表す指標も補助的に設けて「文系寄りか、理系寄りか」を表すことで、全体のデータを上手く解釈できるようになるというわけである。
因子分析の場合の、
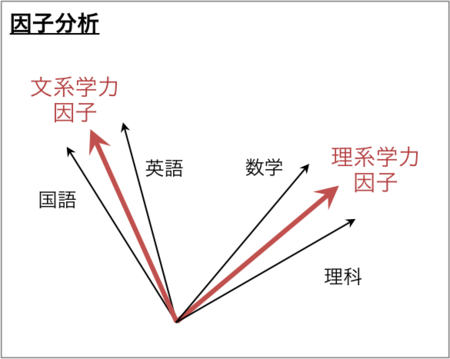
↑この図のようなケースだと、「文系の学力」「理系の学力」という2因子でデータが表現されてるわけだが、これって、文系の学力の反対は理系の学力というわけではない。どっちかというと、反対というよりは「直交」に近いベクトルになっているので、この場合は理系学力と文系学力は「無関係」と言った方がいいだろう。
それに対して、主成分分析の結果が、

↑のような感じだったとすると、「文系・理系傾向」を表す第2主成分は、「理系の反対は文系」になるような指標になっている。つまりデータの解釈自体が、上の因子分析の例とは全く異なるのである。
これらは、そもそも目的も異なるので、どちらがいいということはないだろう。上の例だと因子分析のほうがデータを綺麗に「要約」できているような気もしてしまい、主成分分析よりいいじゃんとか思ってしまうかもしれないが、「総合学力」と「文理傾向」という主成分が得られることで、「賢くて理系寄りの人」「賢くなくて理系寄りの人」「賢くて文系の人」「賢くなくて文系寄りの人」に4分類できたりするので、この解析結果はこれはこれで意味がある。
因子分析は
また、計算方法も主成分分析と因子分析でけっこう異なる*4。
主成分分析の場合は、相関行列から固有値問題を解いたり、分散の最大化問題を解くことにより、淡々と解析的に主成分を求めることができる。それに対して、少なくともこの教科書で解説されている因子分析の例だと、数値計算の繰り返しを行ってモデルを推定することが前提とされている。
……というような比較をしながら考えていたら、「主成分分析」と「因子分析」のそれぞれの本質的な意味合いが、ある程度分かってきたような気がする。
教科書(『多変量解析法入門』第9章)の学習メモ
以下、永田・棟近教科書を読んでいて、注意すべきだったと思った点を順にメモっておく。
とにかく標準化に気をつける
この教科書を読みながた式の展開を追っていく際に、「ん?なんでここはこう変形できるんだっけ?」って一瞬躓くときは、たいてい、「標準化」がポイントになっている。
観測変数が標準化されていると、
- 平均はゼロ
- 分散と標準偏差は1
- 変数の2乗は分散に一致(=1)
- 共分散は相関係数に一致
みたいな性質が出てくるのだが、それはいちいち説明されていないので、最初から頭に入れて読まないと理解できない。
また、少なくともこの第9章で(n-1)というのが出てきたら、それはたいてい、不偏分散の分母に出てくる自由度のことだから、そこに気づいてさえいればとくに数式に疑問を感じることはないだろう。
方向余弦の話
この永田・棟近教科書第9章で文系初学者が躓くとすれば、p.134の、主成分の分散を最大化する際の制約条件の話だ。
主成分は、
で表されるが、これの分散を最大化するための式を展開していって、
・・・(9.7)
が導かれた後に、この関数の最大値を求めるという問題で、
の値は
の値が大きくなればいくらでも大きくなる。そこで、
・・・(9.8)
の制約条件を設けた下で、
の最大化を考える。
という説明が出てくるのだが、「なんでとか
を2乗するんだ???って疑問になる。
(9.7)式が最大値を持たないということは見ればわかるのだが、そのときの制約条件がなぜ(9.8)式の形なのかがさっぱりわからない。
んで、これは調べると(たとえばこのPDF資料)、「方向余弦」というやつに関する定理から導かれていることが分かる。主成分分析の文脈で分かりやすく解説してるページは見つからなかったのだが、だいたい次のような話だと思う。(正確じゃないかも?)
さっきも出した図に少し追記して言うと、
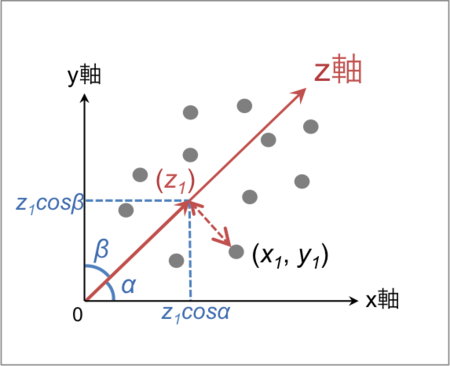
各サンプル値がz軸上に投影されたような感じになり、zという1つの変数で表現されるわけだが、z軸上の点を逆にx、yという元の軸に投影した場合、その座標はそれぞれ、の長さが仮に1だとすれば、
になり、この関係を方向余弦という。で、このベクトルの長さを計算するなどして式をいろいろいじると、を満たすことは容易に分かる。
ということは、z軸上の点というのは、その点をと
で表したときに
を満たすということであり、これはすなわちさっきの主成分の式でいうと、
になるということだ。で、ベクトルを足したりかけたりする計算のやりかたが合っているか知らないんだが(汗)、とか
は分散1のベクトルだから、それを2乗すると1になるはずなので(これは長さであり分散でもある)、
が成り立つという話になるんだろう。たぶん。
この方向余弦の話は、教科書で一切触れられていないので、ちょっと不親切じゃないかと思った。
ラグランジュの未定乗数法の話
上記の分散最大化の計算をするにあたり、ラグランジュの未定乗数法というのが出てくる。文系の私にとっては初耳だが、理系だと最適計算などで頻繁に用いられる超定番の定理らしい。
これは別に難しい話ではなく、元の式と制約条件の式を偏微分して連立方程式をつくるだけの話なので、ネット上の解説を読めば理解できる(たとえばこの資料)。
まぁ、本質的な意味を理解するとか、変数が多くて複雑な場合に実際に計算できるかと言われると心許ないが、公式として覚えれば永田・棟近教科書に出てくる式の展開ぐらいは自分でできるようになる。極値の有無を判別するとかもやらないといけないはずだが、主成分分析をする上ではふつうに極値は存在するものとして計算すればだいたいOKだと思う。
この教科書の計算では、主成分得点の分散を最大化するための計算をするにあたり、ラグランジュの未定乗数法で途中まで計算して式を整理したら、そのまま解き切るのではなく方程式を行列の形に変換して、「固有値問題」として解くという流れになっている。
その他、個別の式の展開や重要事項など
その他、この章を読む上で大事な点、注意すべき点をいくつか。
《分散=固有値》
(9.15)式で、主成分得点の分散は固有値λに等しいというのが出てくるが、これは後の計算でも何度も使うのでとても重要である。あわせて、第1主成分〜第p主成分までに対応するp個の固有値を全部足すとpに一致し、これは変数が標準化されているので分散の合計がpに一致することとあわせて重要であり、一つの主成分が担っている情報量(分散説明率)として「寄与率」を理解する上でも大事である。
《因子負荷量と固有ベクトルの関係》
p.141で「因子負荷量と固有ベクトルは主成分に対して同じ情報量を与える」と書かれてあるが、これは要するに、主成分に因子負荷量をかけたものを足し上げると観測変数を表現することができ、逆に観測変数に固有ベクトルをかけたものを足し上げると主成分になるという、相互的な関係を言っている。
これは、因子分析のモデル式と主成分分析のモデル式を見比べて、なんとなく鏡写しのような構造になっている点を理解する上で重要である。
《主成分をいくつ考慮すべきか》
p.143で、「固有値が1以上」又は「累積寄与率が80%を超える」という目安で主成分を選択(第1主成分から第何主成分までを考慮するか決める)すると書かれてあって、これは主成分1つあたりの固有値の平均が1(それは当たり前だ)だからと説明されているのだが、これもけっきょくそれほど論理的(必然的)な基準ではない点に注意する。
主成分分析も因子分析も結局、「解釈しやすいかどうか」が大事で、その解釈のしやすさは統計学的、数学的に決まるものではない。
ただこの点は、因子分析の方法論の中で、因子数の決定(の目安)に使う「スクリープロット」の見方を理解するときとかにも重要になるので、覚えておくべきではある。
《実際の数値計算》
教科書の、国語・英語・数学・理科の点数を主成分分析する場合の実際の計算結果がp.144に載っているのだが、Rで計算してみると、この教科書に載っている結果とは一部違っていて、第1主成分の固有ベクトルの1つ目と 2つ目の要素の符号が負になる。なんで??
《練習問題》
練習問題で、相関行列をスペクトル分解して固有値を求めたり、因子負荷量を求めたりする計算をやってみると、数式が深く理解できるとともに、こんなの変数が増えたら手計算ではやってられんということが深く痛感できる。