Rでの季節調整をやってみます。
季節調整は、arima関数のseasonal引数を指定したSARIMAモデルや、stl関数でできてそっちは簡単なのですが(参考1・参考2・参考3)、一般的にアメリカ商務省センサス局の「X-12-ARIMA」とか「X-13ARIMA-SEATS」とかが有名なので、それを使ってみようと思います。
1965年に開発された「X-11」は移動平均をつかった成分分解法で、これにRegARIMAモデルをつかって事前にデータ補完する機能などを加えたX-12-ARIMAが1996年に開発され、さらに2012年に、X-11とは別系統の技術として利用されてきたARIMAモデルベースの分解方法であるSEATSを選択肢として使えるようにしたX-13ARIMA-SEATSがリリースされた……ということらしい。なのでX-13はX-12が新しくなったというより、X-12とは別の技術も使えるようにしたパッケージという感じのようです。
X-12-ARIMAは、大きく分けて、異常値等を除去するための回帰変数の決定とARIMAモデルによる予測値を推計する「事前調整パート(RegARIMA)」、X-11による季節調整を行う「移動平均パート」、季節調整系列の適切性や安定性に関する診断を行う「事後診断パート」の3つのパートから構成されている。
https://www.stat.go.jp/training/2kenkyu/ihou/71/pdf/2-2-712.pdf
ということなんですが、要するに季節調整のコア部分にはX-11が使われ続けていて、X-12というのはそれに便利機能を付加したものというイメージです。
Rのパッケージだけではできないので、インストール方法からメモしておきます。具体的には、X-13ARIMA-SEATSをインストールして、それをRの{seasonal}パッケージからよびだして使う形になります。{x12}というパッケージからも使えるので追加的に後でやります。
(OSはMacで、X-code、commandline tools、homebrewがインストールされていることを前提とします)
まず、X13-ARIMAのコンパイルにはgfortranというコンパイラが必要らしいですが、これはgccに統合されているとのことなので、gccをインストールすればよい。homebrewで入ります。
$ brew install gcc
次に、センサス局のサイトにいって、X13のソースコードをダウンロードしてきます。
X-13ARIMA-SEATS Download Page (Unix/Linux Version) - X-13ARIMA-SEATS Seasonal Adjustment Program - US Census Bureau
このURLにある、「x13ashtmlsrc_V1.1_B39.tar.gz」という圧縮ファイルをダウンロードして、解凍するとフォルダが出てきますので、それを適当な場所に置きます。私は、
~/Library/R
に置きました。
で、この記事に書いてあるのですが、
Compiling X 13ARIMA SEATS from Source for OS X · christophsax/seasonal Wiki · GitHub
コンパイル前に、makefileの中身を少し書き換えないと、エラーが出ます。さっき解凍したフォルダの中に、
makefile.gf
というファイルがあるので、これをテキストエディタで開いて、293行目の"-static"を消します。
削除前:$(LINKER) -static -o $@ $(OBJS) $(LDMAP) $(LIBS) $(LDFLAGS)
削除後:$(LINKER) -o $@ $(OBJS) $(LDMAP) $(LIBS) $(LDFLAGS)
あとはターミナルからmakeすればいいです。
$ cd ~/Library/R/x13ashtmlsrc_V1.1_B39
$ make -f makefile.gf
コンパイルが終わると、フォルダの中に
x13asHTMLv11b39
という実行ファイルが出てきます。こいつがX13-ARIMAの処理をやってくれるのですが、Rの{seasonal}パッケージは、ディレクトリを指定してやるとその中にある「x13ashtml」というファイルを探すようになっているので、ファイル名を「x13ashtml」に変えておきます。
$ mv x13asHTMLv11b39 x13ashtml
ここまできたら、あとはRのほうから設定を行います。
> library(seasonal)
> Sys.setenv(X13_PATH = "~/Library/R/x13ashtmlsrc_V1.1_B39")
> checkX13()
X-13 installation test:
- X13_PATH correctly specified
- binary executable file found
- command line test run successful
- command line test produced HTML output
- seasonal test run successful
Congratulations! 'seasonal' should work fine!
上のように、checkX13()を実行して上記のようなメッセージが出たら、セットが成功していて、X13をRから呼び出せるようになっているということになります。インストールに不具合があった場合、ここでエラーが出ます。
季節調整ができるかどうか、肺炎の月別死者数のデータをつかって試してみます。
データは、以下のURLに載っている「人口動態統計月報(概数)」を取りました。平成17年1月から、死因別の死者数が載っていて、前年分も書いてあるので、平成16年1月から数字が手に入りました。
人口動態調査 結果の概要|厚生労働省
なお、2017年1月から死因の分類変更があって、それまで肺炎に分類されていた人が一部、神経系や認知症系の方に分類されるようになったらしくて、内訳をみて揃えることができなかったので、2017年1月以降は1とするダミー変数も作っておきました。あとで外生変数として使います。
データを読み込んで、とりあえず原系列のグラフ描いてみます。
d <- read.csv('source/death.csv')
d <- ts(d, start=c(2004,1), end=c(2019,10), frequency = 12)
plot(d[,2], xlab="", ylab="肺炎死者数", xaxp=c(2004, 2020, 8))

y軸の目盛りの省略が気持ち悪ければylimを設定すればいいと思います。
これに、季節調整をかけてみます。ひとまずダミー変数を使わずに、死者数の系列をそのまま使います。
X-12も含めて季節調整の原理については『入門 季節調整―基礎知識の理解から「X‐12‐ARIMA」の活用法まで』とかに詳しく書いてあります(ちゃんとよんでないけど)。
まずは推定して結果のサマリをみてみます。
> pneu.x13.1 <- seas(x=d[,2])
> summary(pneu.x13.1)
Call:
seas(x = d[, 2])
Coefficients:
Estimate Std. Error z value Pr(>|z|)
Constant 0.022586 0.003928 5.751 0.0000000088872 ***
AO2005.Mar 0.217141 0.032563 6.668 0.0000000000259 ***
LS2015.Feb -0.114776 0.028185 -4.072 0.0000465558118 ***
LS2017.Jan -0.246416 0.027709 -8.893 < 0.0000000000000002 ***
AR-Nonseasonal-01 0.696167 0.052020 13.383 < 0.0000000000000002 ***
MA-Seasonal-12 0.763174 0.053533 14.256 < 0.0000000000000002 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
SEATS adj. ARIMA: (1 0 0)(0 1 1) Obs.: 190 Transform: log
AICc: 2644, BIC: 2665 QS (no seasonality in final): 0
Box-Ljung (no autocorr.): 30.71 Shapiro (normality): 0.9937
Messages generated by X-13:
Warnings:
- At least one visually significant trading day peak has been found in one or more of the estimated
spectra.
「coefficients」の中にある、「AO2005.Mar」というのは、「Additive Outlier」というタイプの異常値が2005年3月に検出されていて、そのダミー変数の係数が推定されてるわけですね。これはいわゆるスパイク的な変化のことでしょう。「LS2015.Feb」と「LS2017.Jan」は「Level Shift」というタイプの異常値が検出されていて、名前はそのまんまで、水準が階段のように上がったり下がったりする変化です。2017年1月のほうは、分類変更の影響です。なおこれらの他に、増減傾向の変化を表す「TC: Trend Change」というタイプの異常値もありますが、これは今回は検出されませんでした。
「ARIMA: (1 0 0)(0 1 1)」とあるのは、いわゆるARIMA(p,d,q)(P,D,Q)の次数ですね。pはARの次数、dは何階和分過程か(何階階差を取って分析するか)、qはMAの次数を表しています。小文字のほうは時系列方向のARIMAの次数で、大文字のほうは季節方向の次数です。季節方向というのは言い方が難しいですが、年を行、月を列とした表とつくった場合に縦方向に眺めるようなイメージで、たとえば2次のAR(2)だったらその部分はYtがY_t-12、Y_t-24で説明されるということです。
「Transform: log」は、デフォルトで自動変換が選択されてて、ここでは対数変換されたようです。対数変換されているばあい、いわゆる「乗法型季節調整」になり、原系列=トレンド成分*季節成分*不規則成分という分解がされていることになります。
グラフを描いてみます。
par(mfrow = c(4,1), oma=c(3,2,2,0), mar=c(0,2,0,2), mgp=c(1,1,0))
plot(pneu.x13.1$series$s10, xlab="", ylab="季節成分", xaxt="n", yaxt="n")
plot(pneu.x13.1$series$s11, xlab="", ylab="季節調整値", xaxt="n", yaxt="n")
plot(pneu.x13.1$series$s12, xlab="", ylab="トレンド成分", xaxt="n", yaxt="n")
plot(pneu.x13.1$series$s13, xlab="", ylab="不規則成分", yaxt="n", xaxp=c(2004, 2020, 8))
par(default.par)
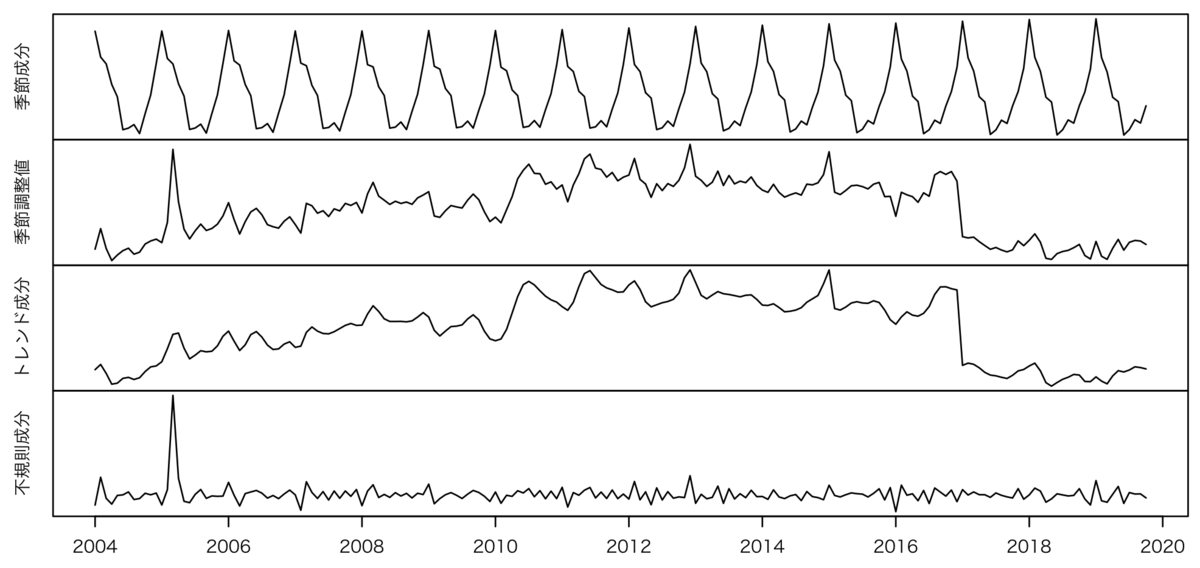
こんな感じ分解されましたが*1、季節調整値(2段目)やトレンド(3段目)をみると、2017年に急激に下がってますね。さきほどの「分類変更」の影響です。
なお、s10とs12とs13をかけると、原系列に戻せます。また、季節調整値というのは、原系列を季節成分で割ったものになります。(そのへんの話はこの資料をみると分かる。)
ここでは貼り付けませんが、季節成分の抽出結果のテーブル(行が年、列が月)を眺めていると、肺炎死者数はやはり2月や1月が多く温かい時期に減りますが、不思議なことに8月は一貫して7月や9月に比べて増える傾向がある。あと、冬場の肺炎死者数と、4月や9・10月といった春秋の肺炎死者数の格差が、年々小さくなっていました(冬場のウェイトが小さくなって春秋のウェイトが大きくなっている)。
ちなみに、推定結果のオブジェクトをそのままplotに投げると、以下のように、原系列と季節調整値を重ねて、かつ3種類のoutlier(異常値)を図示したものが出てきます。
plot(pneu.x13.1)

予測値と信頼区間もついたグラフを描くならこうします。(描画に凝るならggplot2のほうがいいかも)
pneu.x13.f1 <- series(pneu.x13.1, c('forecast.forecasts'))
plot(pneu.x13.1, xlim=c(min(time(d)), max(time(pneu.x13.f1))))
x.ci <- c(time(d)[nrow(d)], time(pneu.x13.f1), rev(time(pneu.x13.f1)), time(d)[nrow(d)])
y.ci <- c(d[nrow(d),2], pneu.x13.f1[,2], rev(pneu.x13.f1[,3]), d[nrow(d),2])
polygon(x.ci, y.ci, col = '#ccccff', border = NA)
pred <- ts(c(d[nrow(d),2], pneu.x13.f1[,1]), start=c(2019,10), end=c(2022,10), frequency=12)
lines(pred, col="#5555ff", lwd=1, lty=1)

次に、2017年1月以降とそれ以前を区別するダミー変数をつかった推定をしてみたいと思ったのですが、なんかエラーが出まくりました。
下記の記事に書いてあるように、外生変数を使う場合、将来予測用に余計なデータが求められて、ややこしいことになるらしい(X13の仕様により)。そこで、x11という引数もあわせて指定すると動くのですが、要するにこれは、成分分解をSEATSではなくX-11で行うということでしょうね。
NOTE not shown · Issue #200 · christophsax/seasonal · GitHub
とりあえずやってみます。
xregという引数に、外生変数を指定します。
> d_sadj.2 <- seas(x=d[,2], xreg=d[,4],
+ forecast.maxlead = "0", series.span=", 2019.10", x11 = "")
> summary(d_sadj.2)
Call:
seas(x = d[, 2], xreg = d[, 4], forecast.maxlead = "0", series.span = ", 2019.10",
x11 = "")
Coefficients:
Estimate Std. Error z value Pr(>|z|)
xreg -0.246421 0.027708 -8.894 < 0.0000000000000002 ***
Constant 0.022586 0.003928 5.750 0.0000000089088 ***
AO2005.Mar 0.217145 0.032563 6.668 0.0000000000259 ***
LS2015.Feb -0.114767 0.028183 -4.072 0.0000465725741 ***
AR-Nonseasonal-01 0.696129 0.052021 13.382 < 0.0000000000000002 ***
MA-Seasonal-12 0.763082 0.053542 14.252 < 0.0000000000000002 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
X11 adj. ARIMA: (1 0 0)(0 1 1) Obs.: 190 Transform: log
AICc: 2644, BIC: 2665 QS (no seasonality in final): 0
Box-Ljung (no autocorr.): 30.71 Shapiro (normality): 0.9937
Messages generated by X-13:
Notes:
- Unable to test LS2017.Jan due to regression matrix singularity.
- Unable to test LS2017.Jan due to regression matrix singularity.
xregが説明変数として導入したダミー変数で、係数は先ほどのLS2017.Janとほぼ同じ値になってますね。そしてLS2017.Jan は消えています。(一番下のNotesに、重複するので削る旨が書いてあります。)
次にグラフです。
par(mfrow = c(4,1), oma=c(3,2,2,0), mar=c(0,2,0,2), mgp=c(1,1,0))
plot(d_sadj.2$series$d10, xlab="", ylab="季節成分", xaxt="n", yaxt="n")
plot(d_sadj.2$series$d11, xlab="", ylab="季節調整値", xaxt="n", yaxt="n")
plot(d_sadj.2$series$d12, xlab="", ylab="トレンド成分", xaxt="n", yaxt="n")
plot(d_sadj.2$series$d13, xlab="", ylab="不規則成分", yaxt="n", xaxp=c(2004, 2020, 8))

seriesから取り出す値が「d10」とかになってるんですが、これはX-11で分解(decompositionのdかな?)された結果のデータです。SEATSでの分解結果は、さっきやったように、「s10」とかで取り出される。
トレンド成分をみると、2017年1月の分類変更は取り除かれている感じになっています。「季節調整値」だけだと、単なる季節調整の結果なので、分類変更の影響が出てしまいますが。
なお、上では示してませんが、ダミー変数にかかる係数の推定結果とかも格納されてて、将来予測を出すときはそれも使われることになります。
性能とかは判断できませんが、インストールも面倒だし、X13の仕様を詳しく見ないと使いこなせないので、ほかのもっと基本的なパッケージ・関数を使った方が楽な気はしますねw
ちなみに、↑でインストールしたX13のエンジンは、{x12}というパッケージからも使えます。
外生変数を使わないなら、{x12}のほうがplotの描き方が楽でいいと思いました。
library(x12)
x12path("~/Library/R/x13ashtmlsrc_V1.1_B39/x13ashtml")
d_x12.1 <- x12(d[,2])
plot(d_x12.1, ylim=c(0, 14200),
original=T, col_original="black",
sa=T, col_sa="blue",
trend=T, col_trend="red", lwd_trend=1.5)
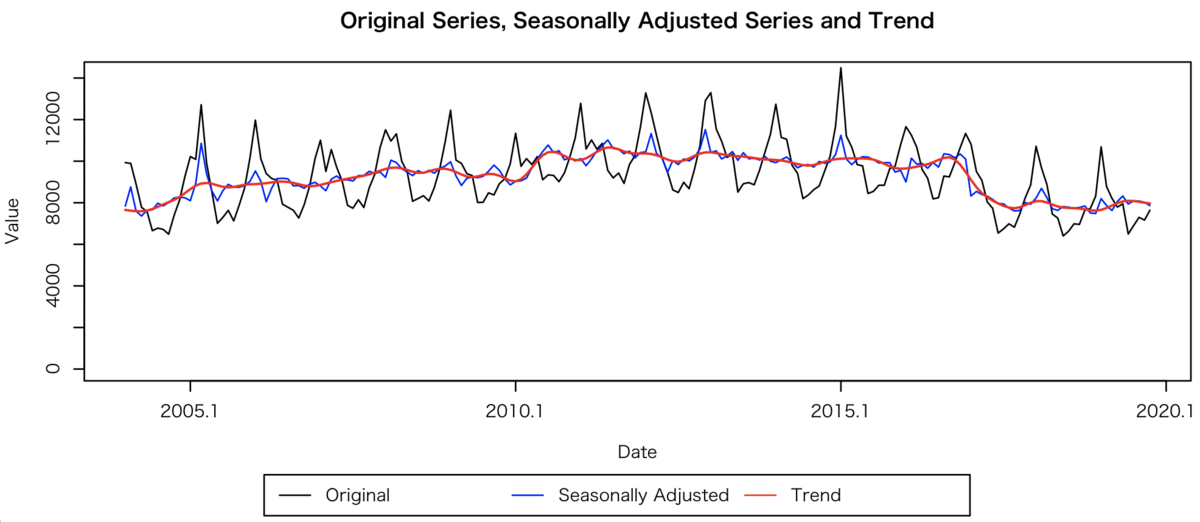
ただ、さっきの分類変更を反映するダミー変数みたいに、回帰の変数を使った推定をしようとするのであれば、設定がいろいろややこしそうです。そもそもX12やX13の機能とシンタックスに関する基礎知識が必要になる模様。
X12やX13の基本が分かっていると、かなりいろいろな要因を季節調整時に考慮できるみたいですが、少し調べたぐらいでは使えそうになかったので、ひとまず放置しました。季節調整を凝らなければならない用事ができたときにまた勉強しようと思います……。
ちなみに自殺者数はこのようになってました。

全体としては減り続けていて、東日本大震災のあった2011年3月に大きく減少し、その後5月に激増しました。